
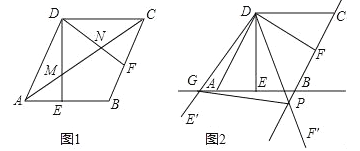
【题目】(2016山东潍坊第24题)如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN=![]() AC;
AC;
(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
【答案】(1)详见解析;(2)将△EDF以点D为旋转中心,顺时针或逆时针旋转60°时,△DGP的面积等于3![]() .
.
【解析】
试题分析:(1)连接BD,易证△ABD为等边三角形,由等腰三角形的三线合一得到AE=EB,根据相似三角形的性质解答即可;(2)分∠EDF顺时针旋转和逆时针旋转两种情况,根据旋转变换的性质解答即可.
试题解析:(1)证明:如图1,连接BD,交AC于O,
在菱形ABCD中,∠BAD=60°,AD=AB,
∴△ABD为等边三角形,
∵DE⊥AB,
∴AE=EB,
∵AB∥DC,
∴![]() =
=![]() =
=![]() ,
,
同理,![]() =
=![]() ,
,
∴MN=![]() AC;
AC;
(2)解:∵AB∥DC,∠BAD=60°,
∴∠ADC=120°,又∠ADE=∠CDF=30°,
∴∠EDF=60°,
当∠EDF顺时针旋转时,
由旋转的性质可知,∠EDG=∠FDP,∠GDP=∠EDF=60°,
DE=DF=![]() ,∠DEG=∠DFP=90°,
,∠DEG=∠DFP=90°,
在△DEG和△DFP中,
 ,
,
∴△DEG≌△DFP,
∴DG=DP,
∴△DGP为等边三角形,
∴△DGP的面积=![]() DG2=3
DG2=3![]() ,
,
解得,DG=2![]() ,
,
则cos∠EDG=![]() =
=![]() ,
,
∴∠EDG=60°,
∴当顺时针旋转60°时,△DGP的面积等于3![]() ,
,
同理可得,当逆时针旋转60°时,△DGP的面积也等于3![]() ,
,
综上所述,将△EDF以点D为旋转中心,顺时针或逆时针旋转60°时,△DGP的面积等于3![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
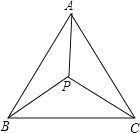
【题目】如图5,点P在正△ABC内一点,∠APB=125°, ∠BPC=100°,则以AP,BP,CP为边长的三角形各内角的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 必然事件发生的概率为1 B. 不可能事件发生的概率为0
C. 随机事件发生的概率大于等于0、小于等于1 D. 概率很小的事件不可能发生
查看答案和解析>>
科目:初中数学 来源: 题型:
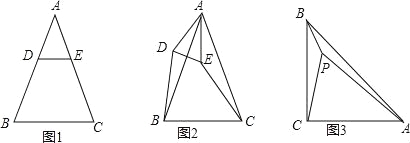
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,等腰Rt△OAB中,∠AOB=90o,等腰Rt△EOF中,∠EOF=90o,连结AE、BF.则AE与BF是什么关系?请说明理由.
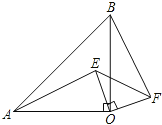
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com