

| A. | 221枚 | B. | 363枚 | C. | 169枚 | D. | 251枚 |
分析 依次解出n=1,2,3,…,图案需要的棋子枚数.再根据规律依此类推,可得出第n个图案需要的棋子枚数,进一步代入求得答案即可.
解答 解:∵n=1时,总数是6+1=7;
n=2时,总数为6×(1+2)+1=19;
n=3时,总数为6×(1+2+3)+1=37枚;
…;
∴n=n时,有6×(1+2+3+…n)+1=6×$\frac{n(n+1)}{2}$+1=3n2+3n+1枚.
∴n=7时,总数为6×(1+2+3…+5+6+7)+1=169枚.
故选:C.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.


科目:初中数学 来源: 题型:解答题
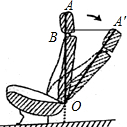 如图,这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O顺时针旋转35°到OA′处,此时点A′到OA的距离为线段A′B的长,求调整后点A′比调整前点A降低的高度AB.(结果取整数)【参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70】
如图,这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O顺时针旋转35°到OA′处,此时点A′到OA的距离为线段A′B的长,求调整后点A′比调整前点A降低的高度AB.(结果取整数)【参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70】查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,AB=6cm,BC=10cm,O是矩形对角线交点,线段OP⊥AD,且OP=4cm,线段OP从图中位置开始,绕点O顺时针旋转一周,线段OP在矩形内部部分(包括端点)的长度y(cm)与点P走过的路程 x(cm)的函数关系式可能是( )
如图,矩形ABCD中,AB=6cm,BC=10cm,O是矩形对角线交点,线段OP⊥AD,且OP=4cm,线段OP从图中位置开始,绕点O顺时针旋转一周,线段OP在矩形内部部分(包括端点)的长度y(cm)与点P走过的路程 x(cm)的函数关系式可能是( )| A. | 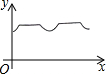 | B. | 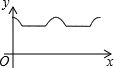 | C. | 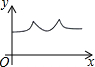 | D. | 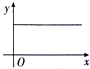 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
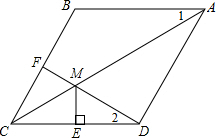 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.
在平面直角坐标系xOy中,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com