
分析 过点A作AF⊥BC于点E,根据AE将梯形ABCD的面积平分,得到梯形ABCD的面积=2△ABE的面积,列出等式即可解答.
解答 解:如图,过点A作AF⊥BC于点E,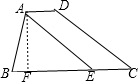
梯形ABCD的面积为:(AD+BC)•AF×$\frac{1}{2}$=(2+6)•AF×$\frac{1}{2}$=4AF,
△ABE的面积为:BE•AF×$\frac{1}{2}$=$\frac{1}{2}$BE•AF,
∵AE将梯形ABCD的面积平分,
∴梯形ABCD的面积=2△ABE的面积,
∴4AF=2×$\frac{1}{2}$BE•AF,
解得:BE=4.
故答案为:4.
点评 本题考查了梯形,解决本题的关键是明确梯形ABCD的面积=2△ABE的面积.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题

| A. | 221枚 | B. | 363枚 | C. | 169枚 | D. | 251枚 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
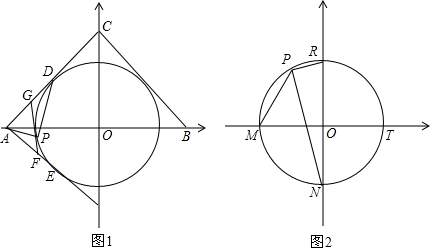
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
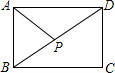 如图,在矩形ABCD中,连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,则下列图象能大致刻画x与y之间的函数关系的是( )
如图,在矩形ABCD中,连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,则下列图象能大致刻画x与y之间的函数关系的是( )| A. | 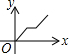 | B. | 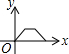 | C. | 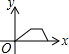 | D. | 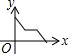 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com