
分析 (1)设S=1+3+32+33+…+3100,两边乘以3得出3S=3+32+33+34+35+…+3100+3101,将下式减去上式即可得出答案;
(2)设S=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{100}}$,两边乘以$\frac{1}{2}$得出$\frac{1}{2}$S=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{101}}$,将下式减去上式即可得出答案.
解答 解:(1)设S=1+3+32+33+…+3100,
两边乘以3得:3S=3+32+33+34+35+…+3100+3101,
将下式减去上式,得3S-S=3101-l
即S=$\frac{{3}^{101}-1}{2}$,
即1+3+32+33+34+…+3100=$\frac{{3}^{101}-1}{2}$
(2)设S=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{100}}$,
两边乘以$\frac{1}{2}$得:$\frac{1}{2}$S=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{101}}$,
将下式减去上式得:-$\frac{1}{2}$S=$\frac{1}{{2}^{101}}$-1,
解得:S=2-$\frac{1}{{2}^{100}}$,
即1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{100}}$=2-$\frac{1}{{2}^{100}}$.
点评 本题考查了有理数的混合运算的应用,能读懂题意是解此题的关键,主要培养学生的理解能力.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
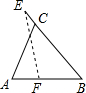 如图,在锐角△ABC中,BC=4,AB=3.5,E为BC延长线上一点,且BE=5,△ABC边上的动点F从点A出发,沿A→B→E的方向运动,到达点E时停止,设点F运动的路程为x,线段EF的长度的平方为y,则y关于x的函数的图象大致为( )
如图,在锐角△ABC中,BC=4,AB=3.5,E为BC延长线上一点,且BE=5,△ABC边上的动点F从点A出发,沿A→B→E的方向运动,到达点E时停止,设点F运动的路程为x,线段EF的长度的平方为y,则y关于x的函数的图象大致为( )| A. | 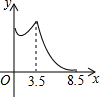 | B. | 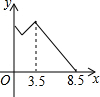 | C. | 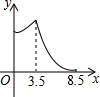 | D. | 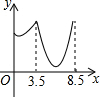 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)2=a2+b2 | B. | (x+6)(x-6)=x2-6 | C. | (x+2)2=x2+2x+4 | D. | (x-y)2=(y-x)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com