
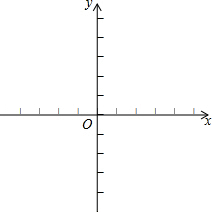 在平面直角坐标系xOy中,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.
在平面直角坐标系xOy中,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.分析 (1)设直线OP和AQ的解析式分别为y=k1x和 y=k2x+b2.由题意得出点Q的坐标为(1,-m),k1=m,$\left\{\begin{array}{l}{k_2}+{b_2}=-m\\ 2{k_2}{+}{b_2}=0\end{array}\right.$,解方程组得出$\left\{\begin{array}{l}{k_2}=m\\{b_2}=-2m\end{array}\right.$,得出k1=k2=m即可,
(2)证明四边形POAQ是菱形,得出PO=AO,由勾股定理得出$\sqrt{1+{m^2}}=2$,得出$m=\sqrt{3}$,即可点P的坐标.
解答 (1)证明:设直线OP和直线AQ的解析式分别为y=k1x和 y=k2x+b2.
根据题意,得:点Q的坐标为(1,-m),k1=m,$\left\{\begin{array}{l}{k_2}+{b_2}=-m\\ 2{k_2}{+}{b_2}=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k_2}=m\\{b_2}=-2m\end{array}\right.$,
∵k1=k2=m,
∴直线OP∥直线AQ;
(2)解:∵OP∥AQ,PB∥OA,AP⊥BO,
∴四边形POAQ是菱形,
∴PO=AO,
∴$\sqrt{1+{m^2}}=2$,
∴$m=±\sqrt{3}$.
∵m>0,
∴$m=\sqrt{3}$,
∴点P的坐标是$({1,\sqrt{3}})$.
点评 本题考查了菱形的判定与性质、一次函数的解析式、勾股定理、坐标与图形性质;熟练掌握菱形的判定与性质,由勾股定理求出m是解决问题(2)的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
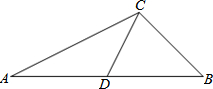 如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{{\sqrt{2}}}{2}$,tanA=$\frac{1}{2}$,BC=2$\sqrt{2}$,求边AB的长和cos∠CDB的值.
如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{{\sqrt{2}}}{2}$,tanA=$\frac{1}{2}$,BC=2$\sqrt{2}$,求边AB的长和cos∠CDB的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 221枚 | B. | 363枚 | C. | 169枚 | D. | 251枚 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
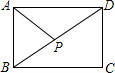 如图,在矩形ABCD中,连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,则下列图象能大致刻画x与y之间的函数关系的是( )
如图,在矩形ABCD中,连接BD,动点P从点B出发,依次沿BD→DC→CB运动至点B停止,设点P的运动路程为x,△APB的面积为y,则下列图象能大致刻画x与y之间的函数关系的是( )| A. | 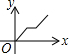 | B. | 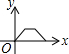 | C. | 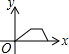 | D. | 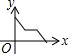 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com