
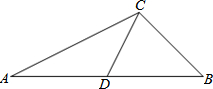
 如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{{\sqrt{2}}}{2}$,tanA=$\frac{1}{2}$,BC=2$\sqrt{2}$,求边AB的长和cos∠CDB的值.
如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{{\sqrt{2}}}{2}$,tanA=$\frac{1}{2}$,BC=2$\sqrt{2}$,求边AB的长和cos∠CDB的值. 分析 CE⊥AB于点E,分别解RT△BCE、RT△ACE求得BE、CE及AE的长,可得AB;根据中线结合BD的长可得DE,在RT△CDE中由勾股定理可得CD,继而计算得cos∠CDB.
解答 解:过点C作CE⊥AB于点E,
在RT△BCE中,∵BC=2$\sqrt{2}$,sinB=$\frac{\sqrt{2}}{2}$,
∴CE=BC•sinB=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2,
∴BE=$\sqrt{B{C}^{2}-C{E}^{2}}$=$\sqrt{(2\sqrt{2})^{2}-{2}^{2}}$=2,
在RT△ACE中,∵tanA=$\frac{1}{2}$,
∴AE=$\frac{CE}{tanA}$=$\frac{2}{\frac{1}{2}}$=4,
∴AB=AE+BE=4+2=6,
∵CD是边AB上的中线,
∴BD=$\frac{1}{2}$AB=3,
∴DE=BD-BE=1,
在RT△CDE中,∵CD=$\sqrt{C{E}^{2}+D{E}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴cos∠CDB=$\frac{DE}{CD}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
故边AB的长为6,cos∠CDB=$\frac{\sqrt{5}}{5}$.
点评 本题主要考查了解直角三角形的能力,构建直角三角形是解题的前提,依据三角函数、勾股定理解直角三角形求出所需线段的长是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | x2+x3=x5 | B. | ($\frac{x}{y}$)2=$\frac{{x}^{2}}{y}$ | C. | x2•x3=x6 | D. | (x2)3=x6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,AB=6cm,BC=10cm,O是矩形对角线交点,线段OP⊥AD,且OP=4cm,线段OP从图中位置开始,绕点O顺时针旋转一周,线段OP在矩形内部部分(包括端点)的长度y(cm)与点P走过的路程 x(cm)的函数关系式可能是( )
如图,矩形ABCD中,AB=6cm,BC=10cm,O是矩形对角线交点,线段OP⊥AD,且OP=4cm,线段OP从图中位置开始,绕点O顺时针旋转一周,线段OP在矩形内部部分(包括端点)的长度y(cm)与点P走过的路程 x(cm)的函数关系式可能是( )| A. | 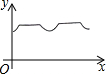 | B. | 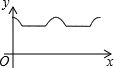 | C. | 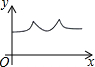 | D. | 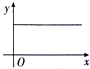 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.
在平面直角坐标系xOy中,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com