【题目】计算
（1）
（2）
【答案】
（1）解： 
=-1+4+1
=4
（2）解： 
= 
【解析】（1）根据乘方的意义，零指数，负指数的意义，分别计算，然后再按有理数的加法法则计算出结果；
（2）先按积的乘方，单项式的乘法法则计算乘法，再合并同类项化为最简形式。
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点，需要掌握零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)才能正确解答此题．
科目：初中数学 来源： 题型：
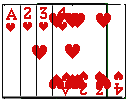
【题目】将如图所示的牌面数字分别是1，2，3，4的四张扑克牌背面朝上，洗匀后放在桌面上，从中随机抽取两张．
（1）用画树状图或列表的方法，列出抽得扑克牌上所标数字的所有可能组合；
（2）求抽得的扑克牌上的两个数字之积的算术平方根为有理数的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
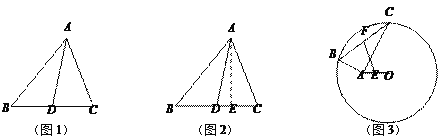
【题目】阅读理解：小明热爱数学，在课外书上看到了一个有趣的定理——“中线长定理”：三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍．如图1，在△ABC中，点D为BC的中点，根据“中线长定理”，可得：
AB2＋AC2＝2AD2＋2BD2．
小明尝试对它进行证明，部分过程如下：
解：过点A作AE⊥BC于点E，如图2，在Rt△ABE中，AB2＝AE2＋BE2，
同理可得：AC2＝AE2＋CE2，AD2＝AE2＋DE2，
为证明的方便，不妨设BD＝CD＝x，DE＝y，
∴AB2＋AC2＝AE2＋BE2＋AE2＋CE2＝……
（1）请你完成小明剩余的证明过程；
理解运用：
（2） ① 在△ABC中，点D为BC的中点，AB＝6，AC＝4，BC＝8，则AD＝_______；
② 如图3，⊙O的半径为6，点A在圆内，且OA＝2
，点B和点C在⊙O上，且∠BAC＝90°，点E、F分别为AO、BC的中点，则EF的长为________；
拓展延伸：
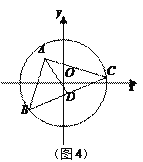
（3）小明解决上述问题后，联想到《能力训练》上的题目：如图4，已知⊙O的半径为5
，以A(3，4)为直角顶点的△ABC的另两个顶点B，C都在⊙O上，D为BC的中点，求AD长的最大值．请你利用上面的方法和结论，求出AD长的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，如图1，再在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒，底面为矩形EFGH，如图2．设小正方形的边长为x厘米．
（1）当矩形纸板ABCD的一边长为90厘米时，求纸盒的侧面积的最大值；
（2）当EH：EF＝7：2，且侧面积与底面积之比为9：7时，求x的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了响应“足球进校园”的目标，某校计划为学校足球队购买一批足球，已知购买2个A品牌的足球和3个B品牌的足球共需380元；购买4个A品牌的足球和2个B品牌的足球共需360元．
（1）求A，B两种品牌的足球的单价．
（2）求该校购买20个A品牌的足球和2个B品牌的足球的总费用．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ） 
A.带①去
B.带②去
C.带③去
D.带①和②去
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com