
����Ŀ�����������Ų�ͬ���ͻij�Ʊ����![]() ������ʾ��������
������ʾ��������![]() ������ʾ��������
������ʾ��������

��1�����ݳ�Ʊ�е���Ϣ��գ����ж���������__________����У�������������ͬ������
��2����֪���ж���������ƽ���ٶȷֱ�Ϊ![]() ��
��![]() �����лij��Ȳ��ƣ�
�����лij��Ȳ��ƣ�
�پ������㣬������л�ֱ���յ㣨����;����ͣ���κ�վ�㣩�������ȶ������絽![]() ����
����![]() ��
��![]() ����֮��ľ��룮
����֮��ľ��룮
���ڢ��в�������ݻ����ϣ���֪![]() ��
��![]() ����;����������
����;����������![]() ��վ��
��վ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
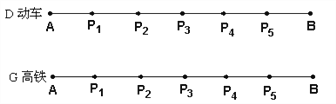
����![]() ������ÿ��վ�㶼ͣ��������ֻͣ��
������ÿ��վ�㶼ͣ��������ֻͣ��![]() ��
��![]() ����վ�㣬���л���ÿ��ͣ��վ�㶼ͣ��
����վ�㣬���л���ÿ��ͣ��վ�㶼ͣ��![]() ������и����϶�����ʱ�̣�
������и����϶�����ʱ�̣�
���𰸡���1��ͬ����2����1200km����8��55��.
�������������������1���ɳ�Ʊ���Եó���������������A�ؿ���B�أ����Զ���������ͬ����У���2�������ȶ���������1��Сʱ�����Զ����ȸ���ȫ�̶��2��Сʱ����A��B���ؾ���Ϊxkm������з���![]() ��
��![]() =2�����x��������3��ÿ������վ�����Ϊ��1200��6=200km��
=2�����x��������3��ÿ������վ�����Ϊ��1200��6=200km��
������ÿվ����ʱ��Ϊ��200��300=![]() h=40min��������ÿվ����ʱ��Ϊ��200��200=1h=60min��
h=40min��������ÿվ����ʱ��Ϊ��200��200=1h=60min��
��������������ÿһվ��ʱ��ͼ���ɴ˿��Եó�������P2��P3֮���ϲ��������������������yСʱ���϶�������y��![]() ����300=��y+1��
����300=��y+1��![]() ��2����200�����y=
��2����200�����y=![]() .
.
���Ը����ھ���![]() h������϶������ϵ�ʱ��Ϊ8��55��.
h������϶������ϵ�ʱ��Ϊ8��55��.
���������
��1��ͬ��
��2������A��B���ؾ���Ϊxkm����
![]() ��
��![]() =2�����x=1200��
=2�����x=1200��
����A��B����֮��ľ���Ϊ1200km��
��ÿ������վ�����Ϊ��1200��6=200km��
������ÿվ����ʱ��Ϊ��200��300=![]() h=40min��������ÿվ����ʱ��Ϊ��200��200=1h=60min��
h=40min��������ÿվ����ʱ��Ϊ��200��200=1h=60min��
���Զ���������ÿһվ��ʱ����ͼ��ʾ��

�ɴ˿��Եó�������P2��P3֮���ϲ�����������
���������yСʱ���϶�����
����y��![]() ����300=��y+1��
����300=��y+1��![]() ��2����200�����y=
��2����200�����y=![]() .
.
���Ը����ھ���![]() h������϶������ϵ�ʱ��Ϊ8��55��.
h������϶������ϵ�ʱ��Ϊ8��55��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɽ���Ͷ����Ͼ�ͳ�ƣ�����ʮһ�塱ĩ��ȫ���ۼƲμӸ������ϱ����������ﵽ88.2���ˣ��ȡ�ʮ�塱ĩ����37.7���ˣ��μӸ���ҽ�Ʊ����������ﵽ130.5���ˣ�������130.5���ÿ�ѧ����������ȷ��ʮ��λ����ʾΪ�� ��
A.1.3��102
B.1.305��106
C.1.3��106
D.1.3��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ε�һ���ڽǵ�ƽ���߰Ѿ��ε�һ���߷ֳ�3cm��5cm�����Σ���þ��ε��ܳ�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AE=CG��BF=DH������EF��FG��GH��HE����֤���ı���EFGH��ƽ���ı��Σ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������н�������Ŀհ״������ʵ������������������ɻ���ѧ����ʽ��
��ͼ����֪AB��CD��BE��CF�ֱ�ƽ����ABC����DCB����֤��BE��CF��

֤����
��AB��CD������֪��
���_____=��_____���� ��
�� ������֪��
���EBC=![]() ��ABC�����ǵ�ƽ���߶��壩
��ABC�����ǵ�ƽ���߶��壩
ͬ������FCB= ��
���EBC=��FCB������ʽ���ʣ�
��BE��CF���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����һ��أ���֪AD=4�ף�CD=3�ף���ADC=90�㣬AB=13�ף�BC=12�ף������ص������ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
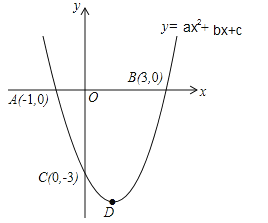
����Ŀ����ͼ��������![]() ��ͼ����x�ύ��A����1.0����B��3��0�����㣬��y�ύ�ڵ�C��0����3��������ΪD��
��ͼ����x�ύ��A����1.0����B��3��0�����㣬��y�ύ�ڵ�C��0����3��������ΪD��
��1����������ߵĽ���ʽ��
��2����������߶���D������ͶԳ��ᣮ
��3��̽���Գ������Ƿ����һ��P��ʹ���Ե�P��D��AΪ������������ǵ��������Σ������ڣ���������з���������P������꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��4��17�գ�����ͳ�ƾֹ���2019��һ�����й��������ݣ��������㣬һ���ȹ���������ֵ213433��Ԫ�����ɱȼ۸���㣬ͬ������6.4%������213433���ÿ�ѧ��������ʾӦΪ��������
A.2.13433��1013B.0.213433��1014
C.213.433��1012D.2.13433��1014
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com