
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.
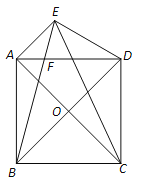
(1)求证:DE=DF;
(2)求证:AE∥BD;
(3)求tan∠ACE的值.
【答案】(1)证明见解析(2)证明见解析 (3)![]()
【解析】试题分析:(1)根据旋转的性质和等腰三角形的性质易得∠BDE=∠BED=75°,根据正方形的性质可得∠ADB=45°,所以∠EDF=30°,在△DEF中,根据三角形的内角和定理可得∠DFE=75°,所以∠DFE=∠DEF,即可得DE=DF ;(2)过点E作EG⊥BD于点G,易证四边形AOGE是矩形,即可得结论;(3)设EG=x,则BE=BD=AC=2EG=2x, Rt△BEG中,由勾股定理可得BG= ![]() ,即可得OG=(
,即可得OG=(![]() )x,再由AE=OG即可得结论.
)x,再由AE=OG即可得结论.
试题解析:
(1)∵BD绕点B逆时针旋转30°至BE,
∴∠DBE=30°,BD=BE,
∴∠BDE=∠BED=![]() =75°
=75°
在正方形ABCD中,BD是对角线,
∴∠ADB=45°,
∴∠EDF=75°-45°=30°,
在△DEF中,∠DFE=180°-∠EDF-∠FED
=180°-30°-75°
=75°
∴∠DFE=∠DEF
∴DE=DF
(2)证明:过点E作EG⊥BD于点G,
∵∠DBE=30°
∴EG= ![]()
在正方形ABCD中,AC、BD是对角线,
∴AC=BD,OA= ![]() ,AC⊥BD
,AC⊥BD
∴EG=OA且EG∥OA
∴四边形AOGE是平行四边形,
∴四边形AOGE是矩形
∴AE∥BD
(3)设EG=x,
则BE=BD=AC=2EG=2x,
Rt△BEG中,BG= ![]() ,
,
∴OG=BG-BO=(![]() )x,
)x,
在矩形AOGE中,∠EAO=90°
AE=OG=(![]() )x
)x
∴tan∠ACE=![]()


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )

A.24 B.12 C.6 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军和小颖对小区学生早上上学到校方式进行了调查,小军将调查结果整理后绘制成如图条形统计图,A代表自行车,B代表步行,C代表乘车. 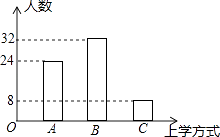
(1)小军和小颖一共调查了多少人?
(2)小颖想将调查结果绘制成扇形统计图,求扇形统计图中C部分对应的扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C.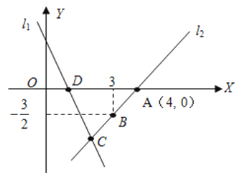
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com