
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�����A����![]() ��0��������ֱ�߷ֱ�y����B��C���㣬��B��C�����������ֱ���һԪ���η���x2��2x��3=0��������
��0��������ֱ�߷ֱ�y����B��C���㣬��B��C�����������ֱ���һԪ���η���x2��2x��3=0��������
��1�����߶�BC�ij��ȣ�
��2�����ʣ�ֱ��AC��ֱ��AB�Ƿ�ֱ����˵�����ɣ�
��3������D��ֱ��AC�ϣ���DB=DC�����D�����ꣻ
��4���ڣ�3���������£�ֱ��BD���Ƿ���ڵ�P��ʹ��A��B��P����Ϊ������������ǵ��������Σ������ڣ���ֱ��д��P������ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��4����2��AC��AB�����ɼ���������3��D����2![]() ��1������4����P������Ϊ����3
��1������4����P����������3![]() ��0��������
��0��������![]() ��2��������3��3��
��2��������3��3��![]() ������3��3+
������3��3+![]() ����
����
��������
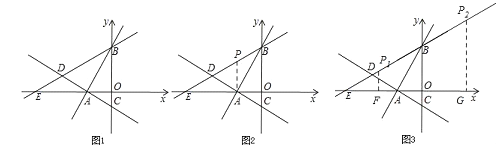
�����������1��������̺������B��C��������꣬�������BC�ij��ȣ���2����A��B��C���������֪OA2=OCOB�����Կ�֤����AOC�ס�BOA�����ö�Ӧ����ȼ��������CAB=90������3���������ֱ��AC�Ľ���ʽ����DB=DC��֪����D��BC�Ĵ�ֱƽ�����ϣ�����D��������Ϊ1���������ֱ��AC�Ľ���ʽ�������D�����ꣻ��4��A��B��P����Ϊ������������ǵ��������Σ��ɷ�Ϊ���������������AB=AP����AB=BP����AP=BP��Ȼ��ֱ����P�����꼴�ɣ�
�����������1����x2��2x��3=0��
��x=3��x=��1��
��B��0��3����C��0����1����
��BC=4��
��2����A����![]() ��0����B��0��3����C��0����1����
��0����B��0��3����C��0����1����
��OA=![]() ��OB=3��OC=1��
��OB=3��OC=1��
��OA2=OBOC��
�ߡ�AOC=��BOA=90����
���AOC�ס�BOA��
���CAO=��ABO��
���CAO+��BAO=��ABO+��BAO=90����
���BAC=90����
��AC��AB��
��3����ֱ��AC�Ľ���ʽΪy=kx+b��
��A����![]() ��0����C��0����1������y=kx+b��
��0����C��0����1������y=kx+b��
��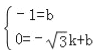 ��
��
��ã�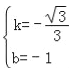 ��
��
��ֱ��AC�Ľ���ʽΪ��y=��![]() x��1��
x��1��
��DB=DC��
����D���߶�BC�Ĵ�ֱƽ�����ϣ�
��D��������Ϊ1��
����y=1����y=��![]() x��1��
x��1��
��x=��2![]() ��
��
��D����������2![]() ��1����
��1����
��4����ֱ��BD�Ľ���ʽΪ��y=mx+n��ֱ��BD��x�ύ�ڵ�E��
��B��0��3����D����2![]() ��1������y=mx+n��
��1������y=mx+n��
��![]() ��
��
��ã�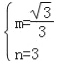
��ֱ��BD�Ľ���ʽΪ��y=![]() x+3��
x+3��
��y=0����y=![]() x+3��
x+3��
��x=��3![]() ��
��
��E����3![]() ��0����
��0����
��OE=3![]() ��
��
��tan��BEC=![]() =
=![]() ��
��
���BEO=30����
ͬ������ã���ABO=30����
���ABE=30����
��PA=ABʱ����ͼ1��
��ʱ����BEA=��ABE=30����
��EA=AB��
��P��E�غϣ�
��P����������3![]() ��0����
��0����
��PA=PBʱ����ͼ2��
��ʱ����PAB=��PBA=30����
�ߡ�ABE=��ABO=30����
���PAB=��ABO��
��PA��BC��
���PAO=90����
����P�ĺ�����Ϊ��![]() ��
��
��x=��![]() ����y=
����y=![]() x+3��
x+3��
��y=2��
��P����![]() ��2����
��2����
��PB=ABʱ����ͼ3��
���ɹ��ɶ�������ã�AB=2![]() ��EB=6��
��EB=6��
����P��y�����ʱ���Ǵ�ʱ��PΪP1��
����P1��P1F��x���ڵ�F��
��P1B=AB=2![]() ��
��
��EP1=6��2![]() ��
��
��sin��BEO=![]() ��
��
��FP1=3��![]() ��
��
��y=3��![]() ����y=
����y=![]() x+3��
x+3��
��x=��3��
��P1����3��3��![]() ����
����
����P��y����Ҳ�ʱ���Ǵ�ʱ��PΪP2��
����P2��P2G��x���ڵ�G��
��P2B=AB=2![]() ��
��
��EP2=6+2![]() ��
��
��sin��BEO=![]() ��
��
��GP2=3+![]() ��
��
��y=3+![]() ����y=
����y=![]() x+3��
x+3��
��x=3��
��P2��3��3+![]() ����
����
������������A��B��P����Ϊ������������ǵ���������ʱ����P������Ϊ����3![]() ��0��������
��0��������![]() ��2��������3��3��
��2��������3��3��![]() ������3��3+
������3��3+![]() ����
����


 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������и����ĺ������滮�����64000000ƽ���ף���64000000�ÿ�ѧ��������ʾΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ�����ľ���ֵ������������෴������ô�����һ���ǣ� ��
A. ���� B. ���� C. ������ D. �Ǹ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������濴Բ���ʹ����濴Բ������״��һ���ģ�����Բ���������ǵĸ���ͼ��������ģ���������________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����IJ��ϣ���A��B�������Ϸֱ��ʾʵ��a��b��A��B����֮��ľ����ʾΪ|AB|����A��B��������һ����ԭ��ʱ�����A��ԭ�㣬��ͼ��|AB|=|OB|=|b|=|a-b|��
��A��B���㶼����ԭ��ʱ����1����ͼ������A��B����ԭ����ұߣ�|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|��2����ͼ������A��B����ԭ�����ߣ�|AB|=|OB|-|OA|=|b|-|a|= -b-��-a��=|a-b|��3����ͼ������A��B��ԭ������ߣ�|AB|=|OA|+|OB|=|a|+|b|=a+��-b��=|a-b|������������������A��B����֮��ľ���|AB|=|a-b|���������֪ʶ�����������⣺
��1�������ϱ�ʾ1��5������֮��ľ�����______�������ϱ�ʾ-2��-4������֮��ľ�����______�������ϱ�ʾ1��-3������֮��ľ�����______��
��2�������ϱ�ʾx��-1������A��B֮��ľ�����______�����|AB|=2����ôxΪ______��
��3����|x+1|+|x-2|ȡ��Сֵʱ����Ӧ��x��ȡֵ��Χ��______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC����D��BC��һ�㣨����B��C�غϣ�����ADΪһ����AD���Ҳ�����ADE��ʹAD=AE����DAE=��BAC������CE��
��1����ͼ1������BAC=90����
����֤����ABD�ա�ACE�������BCE�Ķ�����
��2�����BAC=������BCE=������ͼ2����������֮����������������ϵ����ֱ��д����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ������꼶1�������������100�ײ��ԣ����ɼ�Ϊ15�룬�±���ijС��8�������ijɼ����Լ�¼��������+����ʾ�ɼ�����15�룮
-0.8 | +1 | -1.2 | 0 | -0.7 | +0.6 | -0.4 | -0.1 |
�ʣ���1�����С�������Ĵ����Ϊ���٣�
��2�����С��������ƽ���ɼ��Ƕ����룿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������Ϊ50������,������Ƶ�ʷֲ�ʱ,������Ƶ�����,�����( )
A. 50 B. 0.02 C. 0.1 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=kx��k�dz�����k��0����y��x���������С��д��һ������������k��ֵΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com