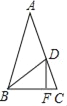
[题目]如图.在△ABC中.AB＝AC.点D在AC上.过点D作DF⊥BC于点F.且BD＝BC＝AD.则∠CDF的度数为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在△ABC中，AB＝AC，点D在AC上，过点D作DF⊥BC于点F，且BD＝BC＝AD，则∠CDF的度数为_____．

【答案】18°

【解析】

设∠A＝α，可得∠ABD＝α，∠C＝∠BDC＝2α，∠ABC＝2α，再根据△ABC中，∠A+∠ABC+∠C＝180°，即可得到∠C的度数，再根据DF⊥BC，即可得出∠CDF的度数．

解：∵AB＝AC，BD＝BC＝AD，

∴∠ACB＝∠ABC，∠A＝∠ABD，∠C＝∠BDC，

设∠A＝α，则∠ABD＝α，∠C＝∠BDC＝2α，∠ABC＝2α，

∵△ABC中，∠A+∠ABC+∠C＝180°，

∴α+2α+2α＝180°，

∴α＝36°，

∴∠C＝72°，

又∵DF⊥BC，

∴Rt△CDF中，∠CDF＝90°﹣72°＝18°，

故答案为：18°．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】某电信公司推出甲、乙两种收费方式供手机用户选择：

甲种方式：每月收月租费5元，每分钟通话费为元；

乙种方式：不收月租费，每分钟通话费为元；

请分别写出甲乙两种收费方式每月付费、元与通话时间分钟之间函数表达式；

如何根据通话时间的多少选择付费方式，请给出你的方案．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】对于平面直角坐标系xOy中的点P（a，b），若点P′的坐标为（a+kb，ka+b）（其中k为常数，且k≠0），

则称点P′为点P的“k属派生点”．例如：P（1，4）的“2属派生点”为P′（1+2×4，2×1+4），即P′（9，6）．

（Ⅰ）点P（﹣2，3）的“3属派生点”P′的坐标为　　；

（Ⅱ）若点P的“5属派生点”P′的坐标为（3，﹣9），求点P的坐标；

（Ⅲ）若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且线段PP′的长度为线段OP长度的2倍，求k的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某公司有火车车皮和货车可供租用，货主准备租用火车车皮和货车运输一批物资，已知以往用这种火车车皮和货车运货情况如下表：

	第一次	第二次
火车车皮（节）	6	8
货车（辆）	15	10
累计运货（吨）	360	440

（1）每节火车车皮和每辆货车平均各装物资多少吨？

（2）若货主需要租用该公司的火车车皮7节，货车10辆，刚好运完这批货物，如按每吨付运费60元，则货主应付运费总额为多少元？

（3）若货主共有300吨货，计划租用该公司的火车车皮或货车正好（每节车皮和每辆货车都满载）把这批货运完，该公司共有哪几种运货方案？写出所有的方案．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，某建筑物AC顶部有一旗杆AB，且点A，B，C在同一条直线上，小明在地面D处观测旗杆顶端B的仰角为30°，然后他正对建筑物的方向前进了20米到达地面的E处，又测得旗杆顶端B的仰角为60°，已知建筑物的高度AC=12m，求旗杆AB的高度（结果精确到0.1米）．参考数据： ≈1.73， ≈1.41．