
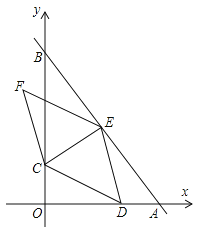
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C在OB上运动,过点C作CE⊥AB于点E;D是x轴上一点,作菱形CDEF,当顶点F恰好落在y轴正半轴上时,点C的纵坐标的值为______.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.
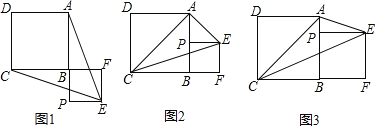
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=m,BP=n,求m:n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用6米的铝合金型材做个如图所示的“日”字形矩形窗框,应做成长,宽各多少米时,才能使做成的矩形窗框透光面积S(平方米)最大,最大透光面积是多少?设矩形窗框的宽为x 米(铝合金型材宽度不计).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,AC于BD交于点O,过点O的MN分到交AB、CD于M、N.

(1)求证:AM+DN=AD;
(2)∠AOM=∠OBC,AC=2![]() ,BD=2
,BD=2![]() ,求MN的长度.
,求MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,BC在直线MN上.
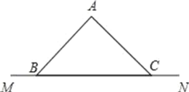
(1)根据下列要求补完整图形,
①画出△ABC关于直线MN对称的三角形A′BC;
②在线段BC上取两点D、E(![]() ,
,![]() ),使BD=CE,连接AD、AE、A′D、A′E;
),使BD=CE,连接AD、AE、A′D、A′E;
(2)求证:四边形ADA′E是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知PA=PB=PC=4,∠BPC=120°,PA∥BC,以AB、PB为邻边作平行四边形ABPD,连接CD,则CD的长为_____________________.
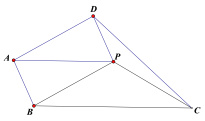
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+bx+c过A(2,0)、C(0,4)两点.
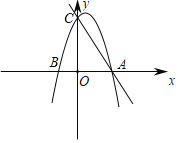
(1)分别求该抛物线和直线AC的解析式;
(2)横坐标为m的点P是直线AC上方的抛物线上一动点,△APC的面积为S.
①求S与m的函数关系式;
②S是否有最大值?若存在,求出最大值,若不存在,请说明理由.
(3)点M是直线AC上一动点,ME垂直x轴于E,在y轴(原点除外)上是否存在点F,使△MEF为等腰直角三角形?若存在,直接写出对应的点F,M的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com