
【题目】如图,抛物线y=﹣2x2+bx+c过A(2,0)、C(0,4)两点.
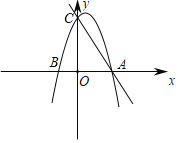
(1)分别求该抛物线和直线AC的解析式;
(2)横坐标为m的点P是直线AC上方的抛物线上一动点,△APC的面积为S.
①求S与m的函数关系式;
②S是否有最大值?若存在,求出最大值,若不存在,请说明理由.
(3)点M是直线AC上一动点,ME垂直x轴于E,在y轴(原点除外)上是否存在点F,使△MEF为等腰直角三角形?若存在,直接写出对应的点F,M的坐标;若不存在,说明理由.
【答案】(1)y=﹣2x+4;y=﹣2x2+2x+4;(2)①S△APC=﹣2m2+4m,②m=1时,△APC的面积为S有最大值,最大值为2;(3)存在.点F坐标为(0,![]() )时,点M的坐标为(
)时,点M的坐标为(![]() ,
,![]() ),点F坐标为(0,﹣4)时,点M的坐标为(4,﹣4);点F坐标为(0,1),点M的坐标为(1,2). 理由见解析.
),点F坐标为(0,﹣4)时,点M的坐标为(4,﹣4);点F坐标为(0,1),点M的坐标为(1,2). 理由见解析.
【解析】
(1)根据待定系数法求解即可;
(2)①过点P作PH∥y轴交AC于点H,则S△APC=S△PHC+S△PHA![]() ,用m的代数式表示出PH的长,而OA=2,整理即得结果;②求由①得到的函数关系式的最大值即可;
,用m的代数式表示出PH的长,而OA=2,整理即得结果;②求由①得到的函数关系式的最大值即可;
(3)根据点M在直线y=-2x+4上,可设点M的坐标为(a,﹣2a+4),然后分∠EMF=90°和∠MFE=90°两种情况,分别根据点M到坐标轴的距离相等和等腰直角三角形的性质列式求解即可.
解:(1)设直线AC的解析式为y=kx+b,
∵A(2,0)、C(0,4),
∴![]() ,解得:
,解得:![]() ,
,
∴直线AC的解析式为y=﹣2x+4;
又∵抛物线y=﹣2x2+bx+c过A(2,0)、C(0,4)两点,
∴![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为y=﹣2x2+2x+4;
(2)①设P的坐标为(m,﹣2m2+2m+4),
如图1,过点P作PH∥y轴交AC于点H,则H(m,﹣2m+4),
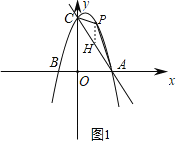
∴PH=﹣2m2+2m+4﹣(﹣2m+4)=﹣2m2+4m,
∵S△APC=S△PHC+S△PHA,
∴![]() =﹣2m2+4m.
=﹣2m2+4m.
②∵0<m<2,S=﹣2m2+4m=﹣2(m﹣1)2+2,
∴m=1时,△APC的面积为S有最大值,最大值为2.
(3)存在.
理由如下:如图2,∵点M在直线y=﹣2x+4上,
∴设点M的坐标为(a,﹣2a+4),
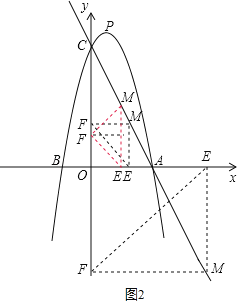
①∠EMF=90°时,∵△MEF是等腰直角三角形,
∴|a|=|﹣2a+4|,
即a=﹣2a+4或a=﹣(﹣2a+4),
解得a=![]() 或a=4,
或a=4,
∴点F坐标为(0,![]() )时,点M的坐标为(
)时,点M的坐标为(![]() ,
,![]() ),
),
点F坐标为(0,﹣4)时,点M的坐标为(4,﹣4);
②∠MFE=90°时,∵△MEF是等腰直角三角形,
∴|a|=![]() |﹣2a+4|,
|﹣2a+4|,
即a=﹣![]() (﹣2a+4)或a=
(﹣2a+4)或a=![]()
当a=﹣![]() (﹣2a+4)时,解得a=1,﹣2a+4=2×1=2,
(﹣2a+4)时,解得a=1,﹣2a+4=2×1=2,
此时,点F坐标为(0,1),点M的坐标为(1,2),
当a=![]() 时,方程无解,
时,方程无解,
综上所述,点F坐标为(0,![]() )时,点M的坐标为(
)时,点M的坐标为(![]() ,
,![]() ),
),
点F坐标为(0,﹣4)时,点M的坐标为(4,﹣4);
点F坐标为(0,1),点M的坐标为(1,2).


科目:初中数学 来源: 题型:
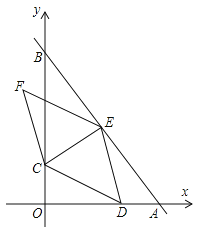
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C在OB上运动,过点C作CE⊥AB于点E;D是x轴上一点,作菱形CDEF,当顶点F恰好落在y轴正半轴上时,点C的纵坐标的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.
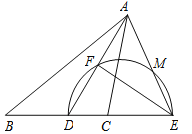
(1)判断AF与DF的数量关系,并说明理由.
(2)只用无刻度的直尺画出△ADE的边DE上的高AH(不要求写做法,保留作图痕迹) .
(3)若EF=8,DF=6,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的位置如图所示(顶点是网格线的交点)

(1)请画出△ABC向右平移2单位再向下平移3个单位的格点△A1B1C1
(2)画出△ABC绕点O逆时针方向旋转90°得到的△A2B2C2并求出旋转过程中点B到B2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以长为2的线段为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,如图所示.
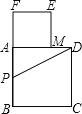
(1)求AM、DM的长;
(2)求证:AM2=ADDM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每位同学都能感受到日出时美丽的景色.下图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,求“图上”太阳升起的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “任意画一个三角形,其内角和为![]() ”是随机事件;
”是随机事件;
B. 某种彩票的中奖率是![]() ,说明每买100张彩票,一定有1张中奖;
,说明每买100张彩票,一定有1张中奖;
C. “篮球队员在罚球线上投篮一次,投中”为随机事件;
D. 投掷一枚质地均匀的硬币100次,正面向上的次数一定是50次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A在x轴上,点B在第一象限内,∠OAB=90°,OA=AB,△OAB的面积为2,反比例函数y=![]() 的图象经过点B.
的图象经过点B.
(1)求k的值;
(2)已知点P坐标为(a,0),过点P作直线OB的垂线l,点O,A关于直线l的对称点分别为O′,A′,若线段O′A′与反比例函数y=![]() 的图象有公共点,直接写出a的取值范围.
的图象有公共点,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
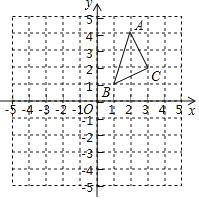
【题目】如图,△ABC的三个顶点的坐标分别是A(2,4),B(1,1),C(3,2).
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标.
(2)已知△A2B2C2与△ABC关于直线l对称,若点C2的坐标为(﹣2,﹣3),请直接写出直线l的函数解析式.注:点A1,B1,C1及点A2,B2,C2分别是点A,B,C按题中要求变换后对应得到的点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com