
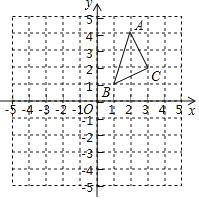
����Ŀ����ͼ����ABC���������������ֱ���A��2��4����B��1��1����C��3��2����
��1��������ABC����ƽ��4����λ���Ⱥ�õ��ġ�A1B1C1����д����C1�����꣮
��2����֪��A2B2C2���ABC����ֱ��l�Գƣ�����C2������Ϊ����2����3������ֱ��д��ֱ��l�ĺ�������ʽ��ע����A1��B1��C1����A2��B2��C2�ֱ��ǵ�A��B��C������Ҫ��任���Ӧ�õ��ĵ㣮
���𰸡���1����ͼ������������A1B1C1Ϊ������C1����1��2������2����ͼ����A2B2C2Ϊ��������������ֱ��l�ĺ�������ʽΪy����x��
��������
��1�����������ص��ƽ�Ƶ�����д����A��B��C�Ķ�Ӧ��A1��B1��C1�����꣬Ȼ�����õ���A1B1C1��
��2�����ݶԳƵ��ص��ɣ�
�⣺��1����ͼ����A1B1C1Ϊ������C1����1��2����
��2����ͼ����A2B2C2Ϊ������
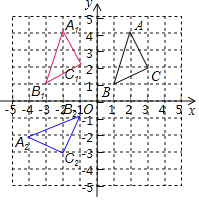
��C��3��2����C2����2����3������A2B2C2���ABC����ֱ��l�Գƣ�
��ֱ��l��ֱƽ��ֱ��CC2��
��ֱ��l�ĺ�������ʽΪy����x��


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y����2x2+bx+c��A��2��0����C��0��4�����㣮
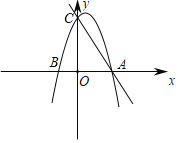
��1���ֱ���������ߺ�ֱ��AC�Ľ���ʽ��
��2��������Ϊm�ĵ�P��ֱ��AC�Ϸ�����������һ���㣬��APC�����ΪS��
����S��m�ĺ�����ϵʽ��
��S�Ƿ������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�
��3����M��ֱ��AC��һ���㣬ME��ֱx����E����y�ᣨԭ����⣩���Ƿ���ڵ�F��ʹ��MEFΪ����ֱ�������Σ������ڣ�ֱ��д����Ӧ�ĵ�F��M�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y��kx+b��ͼ���뷴��������y��![]() ��ͼ���ཻ��A����1��m����B��n����1�����㣮
��ͼ���ཻ��A����1��m����B��n����1�����㣮
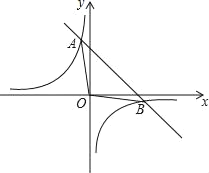
��1��������һ�κ����ı���ʽ��
��2�����OAB�������
��3��ֱ��д��ʹһ�κ���ֵ���ڷ���������ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Anϵ�о���ֽ�ŵĹ�������ǣ��ٸ�����ֽ�Ŷ����ƣ���A1ֽ�Բú���Եõ�����A2ֽ��A2ֽ�Բú���Եõ�����A3ֽ������Anֽ�Բú���Եõ�����An+1ֽ��
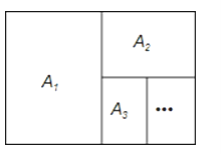
��1����գ�A1ֽ�����A2ֽ����ļ�����A2ֽ�ܳ���A4ֽ�ܳ��ļ�����
��2������Anϵ��ֽ�ŵĹ�������������ϵ��ֽ�ŵij�����������ڿ���֮�ȣ�
��3����A1ֽ�ŵ�����Ϊa�ˣ������A8ֽ�ŵ����������ú�a�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
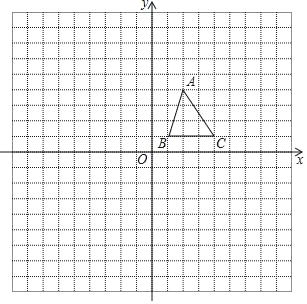
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ������ϵ������������ĵ�λ����Ϊ1����
��1���������ڻ�������ABC�Ե�OΪλ�����ĵ�λ��ͼ����A1B1C1��ʹ��A1B1C1����ABC��λ�Ʊ�Ϊ2��1����A1B1C1λ��y����ࣻ
��2���ֱ�д��A1��B1��C1����������꣺A1�� ����B1�� ����C1�� ����
��3������A1B1C1������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
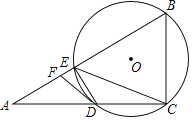
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬D��AC��һ�㣬��B��C��D�������O��AB�ڵ�E������ED��EC����F���߶�AE�ϵ�һ�㣬����FD�����С�FDE����DCE��
��1����֤��DF����O�����ߣ�
��2����D��AC���е㣬��A��30�㣬BC��4����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������εı߳�Ϊ6cm����ȥ�����Ǻ��һ���������Σ�
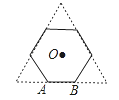
��1��������������εı߳���
��2��������������εı��ľ࣮
��3��������������ε�����ΪO��һ��ΪAB����AB�Ƶ�O��תһ�����õ�ͼ���������ģ�����ͼ��ʾ����������������߶�AB���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=x+2x-3��x���ཻ��A��B���㣬�䶥��ΪM��������������x���·��IJ�����x�ᷭ�ۣ����ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ����ͼ���������ͼ������һ��P����ʹ��S��ABP=6�����P������Ϊ___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC=4������ABC�Ƶ�A˳ʱ����ת30�����õ���ACD���ӳ�AD��BC���ӳ����ڵ�E����DE�ij�Ϊ__________
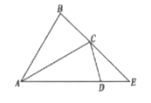
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com