
【题目】如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
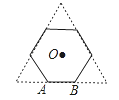
(1)求这个正六边形的边长.
(2)求这个正六边形的边心距.
(3)设这个正六边形的中心为O,一边为AB,则AB绕点O旋转一周所得的图形是怎样的?(作图表示出来)并求出这条线段AB划过的面积.
【答案】(1)正六边形的边长为2;(2)OD=![]() ;(3)线段AB划过的面积为πcm2 .
;(3)线段AB划过的面积为πcm2 .
【解析】
(1)根据题意和正六边形的性质求出正六边形的边长;
(2)求出正六边形的中心角,根据正弦的概念解答即可;
(3)根据题意画出图形,根据圆的面积公式计算即可.
(1)∵六边形DFABGE是正六边形,
∴∠EDF=∠DFA=∠FAB=∠ABG=∠BGE=∠GED=120°,DE=DF,
∴∠ADE=∠AED=60°,
∴△HDE是等边三角形,
∴HD=DE=HE,
同理:FK=KA=AF,
∴HD=DF=FK=2,
∴正六边形的边长为2 cm;
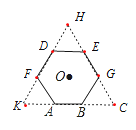
(2)解:连接OA,OB,过点O作ON⊥AB于点N,

∵∠AOB=![]() =60°,
=60°,
∴△OAB是等边三角形,
∴ON=OAsin60°=2×![]() cm;
cm;
(3)如图:
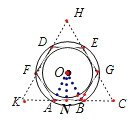
线段AB划过的轨迹是一个圆环,其面积=π×22﹣π×(![]() )2=πcm2 .
)2=πcm2 .


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “任意画一个三角形,其内角和为![]() ”是随机事件;
”是随机事件;
B. 某种彩票的中奖率是![]() ,说明每买100张彩票,一定有1张中奖;
,说明每买100张彩票,一定有1张中奖;
C. “篮球队员在罚球线上投篮一次,投中”为随机事件;
D. 投掷一枚质地均匀的硬币100次,正面向上的次数一定是50次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠ACB=90°,D是BC边上一点,连接AD,分别以CD和AD为直角边作Rt△CDE和Rt△ADF,使∠DCE=∠ADF=90°,点E,F在BC下方,连接EF.
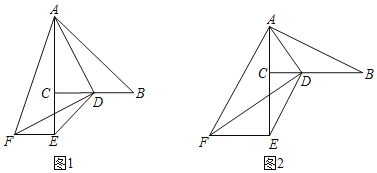
(1)如图1,当BC=AC,CE=CD,DF=AD时,
求证:①∠CAD=∠CDF,
②BD=EF;
(2)如图2,当BC=2AC,CE=2CD,DF=2AD时,猜想BD和EF之间的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
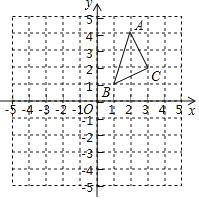
【题目】如图,△ABC的三个顶点的坐标分别是A(2,4),B(1,1),C(3,2).
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标.
(2)已知△A2B2C2与△ABC关于直线l对称,若点C2的坐标为(﹣2,﹣3),请直接写出直线l的函数解析式.注:点A1,B1,C1及点A2,B2,C2分别是点A,B,C按题中要求变换后对应得到的点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,D是△ABC内一点,连接AD,BD.在BD左侧作Rt△BDE,使∠BDE=90°,以AD和DE为邻边作ADEF,连接CD,DF.
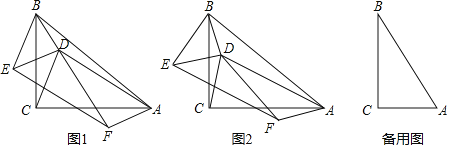
(1)若AC=BC,BD=DE.
①如图1,当B,D,F三点共线时,CD与DF之间的数量关系为 .
②如图2,当B,D,F三点不共线时,①中的结论是否仍然成立?请说明理由.
(2)若BC=2AC,BD=2DE,![]() ,且E,C,F三点共线,求
,且E,C,F三点共线,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
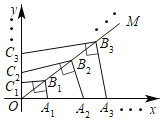
【题目】如图,点A1,A2,A3…,An在x轴正半轴上,点C1,C2,C3,…,![]() 在y轴正半轴上,点B1,B2,B3,…,Bn在第一象限角平分线OM上,OB1=B1B2=B1B3=…=Bn﹣1Bn=
在y轴正半轴上,点B1,B2,B3,…,Bn在第一象限角平分线OM上,OB1=B1B2=B1B3=…=Bn﹣1Bn=![]() a,A1B1⊥B1C1,A2B2⊥B2C2,A3B3⊥B3C3,…,
a,A1B1⊥B1C1,A2B2⊥B2C2,A3B3⊥B3C3,…,![]() ,…,则第n个四边形
,…,则第n个四边形![]() 的面积是____.
的面积是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点C(0,4),交x轴正半轴于点B,连接AC,点E是线段OB上一动点(不与点O,B重合),以OE为边在x轴上方作正方形OEFG,连接FB,将线段FB绕点F逆时针旋转90°,得到线段FP,过点P作PH∥y轴,PH交抛物线于点H,设点E(a,0).

(1)求抛物线的解析式.
(2)若△AOC与△FEB相似,求a的值.
(3)当PH=2时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图,根据图象回答下列问题:
的图象如图,根据图象回答下列问题:
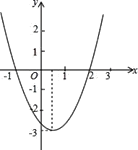
(1)写出方程![]() 的两个根;
的两个根;
(2)写出不等式![]() 的解集;
的解集;
(3)写出不等式![]() 的解集;
的解集;
(4)如果方程![]() 无实数根,求
无实数根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
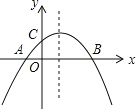
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC;则下列结论:①abc<0;②![]() >0;③ac-b+1=0;④OAOB=-
>0;③ac-b+1=0;④OAOB=-![]() .其中正确的结论( )
.其中正确的结论( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com