
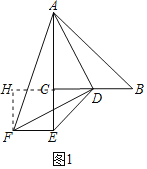
【题目】已知,在Rt△ABC中,∠ACB=90°,D是BC边上一点,连接AD,分别以CD和AD为直角边作Rt△CDE和Rt△ADF,使∠DCE=∠ADF=90°,点E,F在BC下方,连接EF.
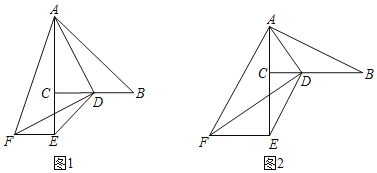
(1)如图1,当BC=AC,CE=CD,DF=AD时,
求证:①∠CAD=∠CDF,
②BD=EF;
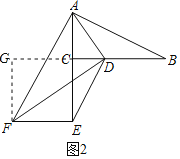
(2)如图2,当BC=2AC,CE=2CD,DF=2AD时,猜想BD和EF之间的数量关系?并说明理由.
【答案】(1)①见解析;②见解析;(2)BD=EF,理由见解析.
【解析】
(1)①根据同角的余角相等证明;
②作FH⊥BC交BC的延长线于H,证明△ACD≌△DHF,根据全等三角形的性质得到DH=AC,结合图形证明即可;
(2)作FG⊥BC交BC的延长线于G,证明△ACD∽△DGF,根据相似三角形的性质得到DG=2AC,证明结论.
(1)证明:①∵∠ACB=90°,
∴∠CAD+∠ADC=90°,
∵∠CDF+∠ADC=90°,
∴∠CAD=∠CDF;
②作FH⊥BC交BC的延长线于H,
则四边形FECH为矩形,
∴CH=EF,
在△ACD和△DHF中,
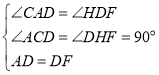 ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ;
;
(2)![]() ,
,
理由如下:作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
则四边形![]() 为矩形,
为矩形,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ,GF=2CD,
,GF=2CD,
∵BC=2AC,CE=2CD,
∴BC=DG,GF=CE,
∴BD=CG,
∵GF∥CE,GF=CE,∠G=90°,
∴四边形FECG为矩形,
∴CG=EF,
∴BD=EF.


科目:初中数学 来源: 题型:
【题目】如图,由4个全等的正方形组成L形图案,请按下列要求画图:
(1)在图①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB、AC是⊙O的弦,AB、AC的长分别等于⊙O的内接正六边形和正五边形的边长.
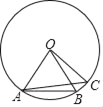
(1)试判断BC的长是否等于⊙O的内接正几边形的边长;
(2)如果⊙O的半径OA=6,求⊙O的内接正六边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A(﹣1,m),B(n,﹣1)两点.
的图象相交于A(﹣1,m),B(n,﹣1)两点.
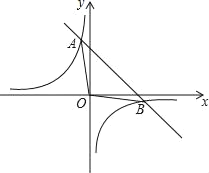
(1)求出这个一次函数的表达式.
(2)求△OAB的面积.
(3)直接写出使一次函数值大于反比例函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是( )
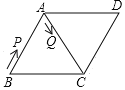
A. 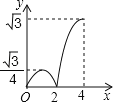 B.
B. 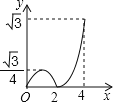
C. 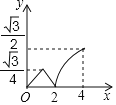 D.
D. 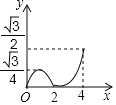
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,An系列矩形纸张的规格特征是:①各矩形纸张都相似;②A1纸对裁后可以得到两张A2纸,A2纸对裁后可以得到两张A3纸,…,An纸对裁后可以得到两张An+1纸.
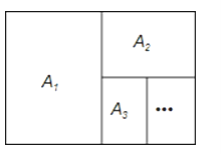
(1)填空:A1纸面积是A2纸面积的几倍,A2纸周长是A4纸周长的几倍;
(2)根据An系列纸张的规格特征,求出该系列纸张的长与宽(长大于宽)之比;
(3)设A1纸张的重量为a克,试求出A8纸张的重量.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
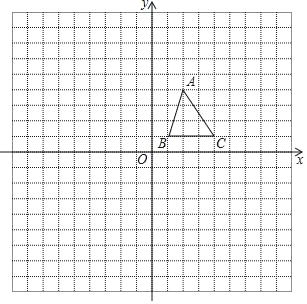
【题目】△ABC在平面直角坐标系中的位置如图所示(坐标系内正方形网格的单位长度为1):
(1)在网格内画出和△ABC以点O为位似中心的位似图形△A1B1C1,使△A1B1C1和△ABC的位似比为2:1且△A1B1C1位于y轴左侧;
(2)分别写出A1、B1、C1三个点的坐标:A1 、B1 、C1 ;
(3)求△A1B1C1的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
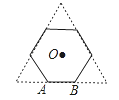
(1)求这个正六边形的边长.
(2)求这个正六边形的边心距.
(3)设这个正六边形的中心为O,一边为AB,则AB绕点O旋转一周所得的图形是怎样的?(作图表示出来)并求出这条线段AB划过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
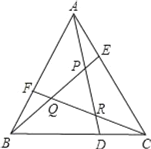
【题目】已知:点D、E、F分别是等边△ABC三边上的三等分点,AD、BE、CF两两相交于P、Q、R点,(如图所示),求△PQR的面积与△ABC面积的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com