
【题目】已知:点D、E、F分别是等边△ABC三边上的三等分点,AD、BE、CF两两相交于P、Q、R点,(如图所示),求△PQR的面积与△ABC面积的比值.
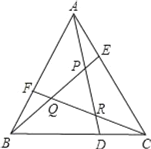
【答案】S△PQR:S△ABC=1:7.
【解析】
可作AG∥BC交BE延长线于点G,作DH∥AB交CF于点H,由平行线分线段成比例可得线段之间的比例关系,进而转化为三角形的面积关系,即可求解结论.
解:作AG∥BC交BE延长线于点G,作DH∥AB交CF于点H,
则得:
AG:BC=AE:EC=1:2,AG:BD=3:4,
又由于DH:BF=1:3,DH:AF=1:6,
所以DR:AR=1:6,DR:DA=1:7,
从而S△CDR=![]() S△BFC=
S△BFC=![]() S△ABC,
S△ABC,
同理可得S△BFQ= S△APE=![]() S△ABC,
S△ABC,
∵S△PQR=S△BCE(S△BCFS△BFQ)(S△ACDS△APES△CDR)=![]() S△ABC-(
S△ABC-(![]() S△ABC
S△ABC ![]() S△ABC)(
S△ABC)(![]() S△ABC
S△ABC ![]() S△ABC
S△ABC ![]() S△ABC)=
S△ABC)=![]() S△ABC
S△ABC
因此S△PQR:S△ABC=1:7.


科目:初中数学 来源: 题型:
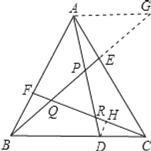
【题目】已知,在Rt△ABC中,∠ACB=90°,D是BC边上一点,连接AD,分别以CD和AD为直角边作Rt△CDE和Rt△ADF,使∠DCE=∠ADF=90°,点E,F在BC下方,连接EF.
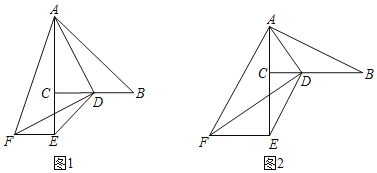
(1)如图1,当BC=AC,CE=CD,DF=AD时,
求证:①∠CAD=∠CDF,
②BD=EF;
(2)如图2,当BC=2AC,CE=2CD,DF=2AD时,猜想BD和EF之间的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点C(0,4),交x轴正半轴于点B,连接AC,点E是线段OB上一动点(不与点O,B重合),以OE为边在x轴上方作正方形OEFG,连接FB,将线段FB绕点F逆时针旋转90°,得到线段FP,过点P作PH∥y轴,PH交抛物线于点H,设点E(a,0).

(1)求抛物线的解析式.
(2)若△AOC与△FEB相似,求a的值.
(3)当PH=2时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图,根据图象回答下列问题:
的图象如图,根据图象回答下列问题:
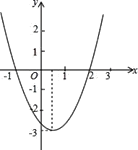
(1)写出方程![]() 的两个根;
的两个根;
(2)写出不等式![]() 的解集;
的解集;
(3)写出不等式![]() 的解集;
的解集;
(4)如果方程![]() 无实数根,求
无实数根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
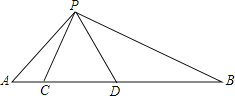
【题目】如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
(1)求∠APB的大小.
(2)说明线段AC、CD、BD之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
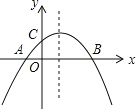
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC;则下列结论:①abc<0;②![]() >0;③ac-b+1=0;④OAOB=-
>0;③ac-b+1=0;④OAOB=-![]() .其中正确的结论( )
.其中正确的结论( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
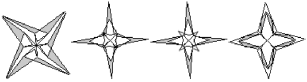
【题目】下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com