
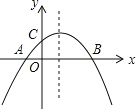
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC;则下列结论:①abc<0;②![]() >0;③ac-b+1=0;④OAOB=-
>0;③ac-b+1=0;④OAOB=-![]() .其中正确的结论( )
.其中正确的结论( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】C
【解析】
利用抛物线开口方向得到a<0,利用抛物线的对称轴位置得到b>0,利用抛物线与y轴的交点位置得到c>0,则可对①进行判断;利用抛物线与x轴有2个交点可对②进行判断;把A点坐标代入解析式可对③进行判断;设A、B两点的横坐标为x1、x2,则OA=-x1,OB=x2,利用根与系数的关系可对④进行判断.
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,
∴![]() <0,所以②错误;
<0,所以②错误;
∵OA=OC,C(0,c),
∴A(-c,0),
∴ac2-bc+c=0,
∴ac-b+1=0,所以③正确;
设A、B两点的横坐标为x1、x2,则OA=-x1,OB=x2,
∵x1x2=![]() ,
,
∴OAOB=-![]() ,所以④正确.
,所以④正确.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
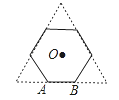
(1)求这个正六边形的边长.
(2)求这个正六边形的边心距.
(3)设这个正六边形的中心为O,一边为AB,则AB绕点O旋转一周所得的图形是怎样的?(作图表示出来)并求出这条线段AB划过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
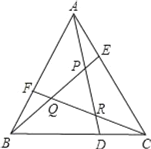
【题目】已知:点D、E、F分别是等边△ABC三边上的三等分点,AD、BE、CF两两相交于P、Q、R点,(如图所示),求△PQR的面积与△ABC面积的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
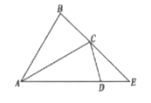
【题目】如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(k+1)x+![]() k2+1=0
k2+1=0
(1) 当k取何值方程有两个实数根
(2) 是否存在k值使方程的两根为一个矩形的两邻边长,且矩形的对角线长为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
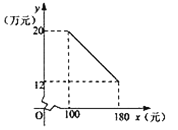
【题目】某科技公司用480万元购得某种产品的生产技术后,并进一步投入资金1520万元购买生产设备,进行该产品的生产加工.已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价不低于100元,但不超过180元.设销售单价为![]() (元),年销售量为
(元),年销售量为![]() (万件),年获利为
(万件),年获利为![]() (万元),该产品年销售量
(万元),该产品年销售量![]() (万件)与产品售价
(万件)与产品售价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数表达式,并写出
之间的函数表达式,并写出![]() 的取值范围;
的取值范围;
(2)求第一年的年获利![]() 与
与![]() 之间的函数表达式,并说明投资的第一年,该公司是盈利还是亏损?并求当盈利最大或亏损最小时的产品售价;
之间的函数表达式,并说明投资的第一年,该公司是盈利还是亏损?并求当盈利最大或亏损最小时的产品售价;
(3)在(2)的条件下.即在盈利最大或亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利不低于1370万元?若能,求出第二年的售价在什么范围内;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究函数![]() 的图象与性质)
的图象与性质)
(1)函数![]() 的自变量x的取值范围是________;
的自变量x的取值范围是________;
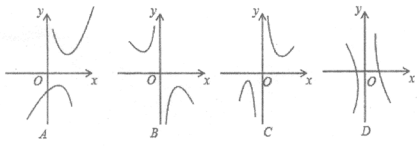
(2)下列四个函数图象中,函数![]() 的图象大致是_______;
的图象大致是_______;
(3)对于函数![]() ,求当x>0时,y的取值范围。请将下面求解此问题的过程补充完整:
,求当x>0时,y的取值范围。请将下面求解此问题的过程补充完整:
解:因为x>0,所以![]()
![]() _________。
_________。
因为![]() ,所以y________。
,所以y________。
(拓展运用)
(4)若函数![]() ,则y的取值范围是_______________________。
,则y的取值范围是_______________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念“五四运动”100周年,某校举行了征文比赛,该校学生全部参加了比赛.比赛设置一等、二等、三等三个奖项,赛后该校对学生获奖情况做了抽样调查,并将所得数据绘制成如图所示的两幅不完整的统计图.根据图中信息解答下列问题:
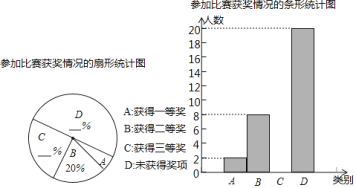
(1)本次抽样调查学生的人数为 .
(2)补全两个统计图,并求出扇形统计图中A所对应扇形圆心角的度数.
(3)若该校共有840名学生,请根据抽样调查结果估计获得三等奖的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com