
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点C(0,4),交x轴正半轴于点B,连接AC,点E是线段OB上一动点(不与点O,B重合),以OE为边在x轴上方作正方形OEFG,连接FB,将线段FB绕点F逆时针旋转90°,得到线段FP,过点P作PH∥y轴,PH交抛物线于点H,设点E(a,0).

(1)求抛物线的解析式.
(2)若△AOC与△FEB相似,求a的值.
(3)当PH=2时,求点P的坐标.
【答案】(1)y=﹣x2+3x+4;(2)a=![]() 或
或![]() ;(3)点P的坐标为(2,4)或(1,4)或(
;(3)点P的坐标为(2,4)或(1,4)或(![]() ,4).
,4).
【解析】
(1)点C(0,4),则c=4,
二次函数表达式为:y=﹣x2+bx+4,
将点A的坐标代入上式得:0=﹣1﹣b+4,解得:b=3,
故抛物线的表达式为:y=﹣x2+3x+4;
(2)tan∠ACO=![]() =
=![]() ,
,
△AOC与△FEB相似,则∠FBE=∠ACO或∠CAO,
即:tan∠FEB=![]() 或4,
或4,
∵四边形OEFG为正方形,则FE=OE=a,
EB=4﹣a,
则![]() 或
或![]() ,
,
解得:a=![]() 或
或![]() ;
;
(3)令y=﹣x2+3x+4=0,解得:x=4或﹣1,故点B(4,0);
分别延长CF、HP交于点N,
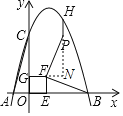
∵∠PFN+∠BFN=90°,∠FPN+∠PFN=90°,
∴∠FPN=∠NFB,
∵GN∥x轴,∴∠FPN=∠NFB=∠FBE,
∵∠PNF=∠BEF=90°,FP=FB,
∴△PNF≌△BEF(AAS),
∴FN=FE=a,PN=EB=4﹣a,
∴点P(2a,4),点H(2a,﹣4a2+6a+4),
∵PH=2,
即:﹣4a2+6a+4﹣4=|2|,
解得:a=1或![]() 或
或![]() 或
或![]() (舍去),
(舍去),
故:点P的坐标为(2,4)或(1,4)或(![]() ,4).
,4).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB、AC是⊙O的弦,AB、AC的长分别等于⊙O的内接正六边形和正五边形的边长.
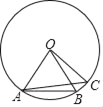
(1)试判断BC的长是否等于⊙O的内接正几边形的边长;
(2)如果⊙O的半径OA=6,求⊙O的内接正六边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
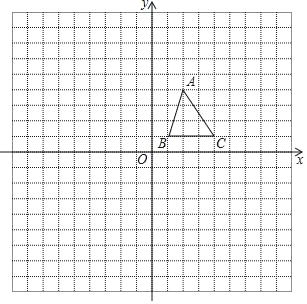
【题目】△ABC在平面直角坐标系中的位置如图所示(坐标系内正方形网格的单位长度为1):
(1)在网格内画出和△ABC以点O为位似中心的位似图形△A1B1C1,使△A1B1C1和△ABC的位似比为2:1且△A1B1C1位于y轴左侧;
(2)分别写出A1、B1、C1三个点的坐标:A1 、B1 、C1 ;
(3)求△A1B1C1的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
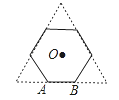
(1)求这个正六边形的边长.
(2)求这个正六边形的边心距.
(3)设这个正六边形的中心为O,一边为AB,则AB绕点O旋转一周所得的图形是怎样的?(作图表示出来)并求出这条线段AB划过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
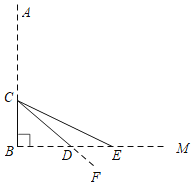
【题目】如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x+2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象,如图.在这个新图象上有一点P,能使得S△ABP=6,则点P的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0、1、2;乙袋中装有3个完全相同的小球,分别标有数字-1、-2、0;先从甲袋中随机取出一个小球,记录标有的数字为x,再从乙袋中随机取出一个小球,记录标有的数字为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x2-1的图象上的概率;
(3)若以点M为圆心,2为半径作⊙M,求⊙M与坐标轴相切的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
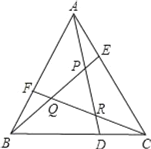
【题目】已知:点D、E、F分别是等边△ABC三边上的三等分点,AD、BE、CF两两相交于P、Q、R点,(如图所示),求△PQR的面积与△ABC面积的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com