
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0、1、2;乙袋中装有3个完全相同的小球,分别标有数字-1、-2、0;先从甲袋中随机取出一个小球,记录标有的数字为x,再从乙袋中随机取出一个小球,记录标有的数字为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x2-1的图象上的概率;
(3)若以点M为圆心,2为半径作⊙M,求⊙M与坐标轴相切的概率.
【答案】(1)答案见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1) 根据题意画出树状图即可.
(2)分别将各点坐标代入函数y=-x2-1解析式, 若等式成立, 则该点在其图象上, 用满足条件的M点的个数除以M点总个数即为所求概率。
(3) 分别计算各点到0点的距离, 若OM> 2, 则在⊙0上或⊙0外, 可以过M点作⊙0的切线,满足条件的M点的个数除以M点总个数即为所求概率.
解:(1) 树状图如图所示, 则M所有可能的坐标有9种情况,分别为:(0,-1),(0,-2),(0,0),(1,-1),(1,-2),(1,0),(2,-1),(2,-2),(2,0).
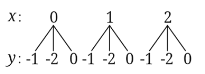
(2) 将 (1) 中的9个坐标分别代入函数y=-x2-1, 可得在函数的图象上的M点有两个: (0,-1), (1,-2),所以点M在函数y=-x2+1的图象上的概率为![]() .
.
(3) 要过M作圆的切线, 则该点应该在圆上或者圆外, 通过比较OM与半径长度可知, 点M在⊙0上或⊙0外的有5个, 分别为(0,-2),(1,-2),(2,-1),(2,-2),(2,0).则过M点能作⊙0的切线的概率为![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
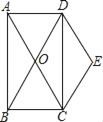
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点C,交AB的延长线于点E,连接CD、CE.
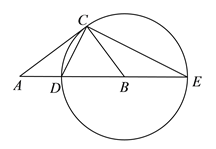
(1)求证:△ACD∽△AEC;
(2)当![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4![]() ,求△ACE的面积.
,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从下列算式:①![]() ;②26÷23=4;③ -12018=1;④ (-
;②26÷23=4;③ -12018=1;④ (-![]() )2=3;⑤a+a=a2中随机抽取一个,运算结果正确的概率是( )
)2=3;⑤a+a=a2中随机抽取一个,运算结果正确的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
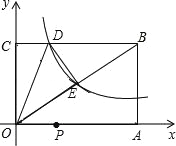
【题目】如图,已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,顶点B的坐标是(6,4),反比例函数y=![]() (x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.
(x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.
(1)①求反比例函数的解析式与点D的坐标;②直接写出△ODE的面积;
(2)若P是OA上的动点,求使得“PD+PE之和最小”时的直线PE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
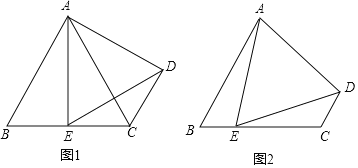
【题目】如图,在四边形ABCD中,AB∥CD,AB=BC,∠B=60°,E是BC边上一点.
(1)如图1,若E是BC的中点,∠AED=60°,求证:CE=CD;
(2)如图2,若∠EAD=60°,求证:△AED是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象开口向上,图象经过点
的图象开口向上,图象经过点![]() 和
和![]() ,且与
,且与![]() 轴相交于负半轴.
轴相交于负半轴.
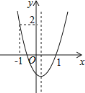
第![]() 问:给出四个结论:①
问:给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .写出其中正确结论的序号(答对得
.写出其中正确结论的序号(答对得![]() 分,少选、错选均不得分)
分,少选、错选均不得分)
第 ![]() 问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)通过配方,写出其对称轴,顶点坐标;
(2)分别求出其与![]() 轴、
轴、![]() 轴的交点坐标;
轴的交点坐标;
(3)画出函数的大致图象,结合图象说明,当![]() 取何值时,
取何值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中“今有勾七步,股有二十四步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为7步,股(长直角边)长为24步,问该直角三角形的容圆(内切圆)直径是多少?”( )
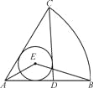
A. 4步 B. 5步 C. 6步 D. 8步
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com