
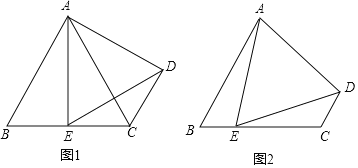
【题目】如图,在四边形ABCD中,AB∥CD,AB=BC,∠B=60°,E是BC边上一点.
(1)如图1,若E是BC的中点,∠AED=60°,求证:CE=CD;
(2)如图2,若∠EAD=60°,求证:△AED是等边三角形.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据AB=BC,∠B=60°得三角形ABC为等边三角形,再根据等边三角形的性质得AE⊥BC,进而证明∠EDC=∠DEC即可;
(2)连接AC,根据两条线平行,同旁内角互补和三角形内角和定理得∠ADC=120°﹣∠BAE,∠AEB=120°﹣∠BAE,即可证明△ABE≌△ACD,进而得结论.
(1)∵AB=BC,∠B=60°,
∴△ABC是等边三角形,
∴∠ACB=60°=∠BAC,
∵E是BC的中点,
∴AE⊥BC,
∴∠AEC=90°,
∵∠AED=60°,
∴∠DEC=30°,
∵AB∥CD,
∴∠ACD=∠BAC=60°,
∴∠ECD=∠ACE+∠ACD=120°,
∴∠CDE=180°﹣120°﹣30°=30°,
∴∠CED=∠CDE,
∴CE=CD.
(2)如图:连接AC,
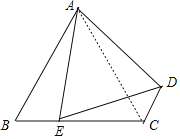
∵AB=BC,∠B=60°,
∴△ABC是等边三角形,
∴AB=AC,
∵AB∥CD,
∴∠BAD+∠ADC=180°,
∵∠EAD=60°,
∴∠ADC=180°﹣∠EAD﹣∠EAB=120°﹣∠EAB.
在△ABE中,∠AEB=180°﹣∠B﹣∠EAB=120°﹣∠EAB,
∴∠AEB=∠ADC,
∵∠BAE+∠EAC=∠DAC+∠EAC=60°,
∴∠BAE=∠DAC,
∴△ABE≌△ACD(AAS),
∴AE=AD,
∠EAD=60°,
∴△AED是等边三角形.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】已知一元二次方程2x2+2x﹣1=0的两个根为x1,x2,且x1<x2,下列结论正确的是( )
A. x1+x2=1 B. x1x2=﹣1 C. |x1|<|x2| D. x12+x1=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0、1、2;乙袋中装有3个完全相同的小球,分别标有数字-1、-2、0;先从甲袋中随机取出一个小球,记录标有的数字为x,再从乙袋中随机取出一个小球,记录标有的数字为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x2-1的图象上的概率;
(3)若以点M为圆心,2为半径作⊙M,求⊙M与坐标轴相切的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
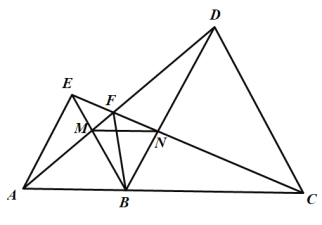
【题目】如图,![]() ,
,![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,下列结论正确的有_________.
,下列结论正确的有_________.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC三边分别为![]() 、
、![]() 、
、![]() ,根据下列条件能判断△ABC为直角三角形的有 ( )
,根据下列条件能判断△ABC为直角三角形的有 ( )
①∠A=∠B+∠C;②∠A:∠B:∠C=3:4:5;③![]() ;④
;④![]() ,
,![]() ,
,![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
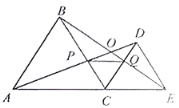
【题目】如图,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 重合),在
重合),在![]() 同侧分别作等边三角形
同侧分别作等边三角形![]() 和等边三角形
和等边三角形![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是等边三角形,恒成立的是______.
是等边三角形,恒成立的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
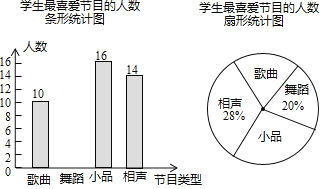
请你根据图中信息,回答下列问题:
(1)本次共调查了 名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于 度.
(3)补全条形统计图(标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为 人.
(5)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com