【题目】如图所示，锐角
中，
，
分别是
，
边上的点，
，
，且
，
、
交于点
，若
，则
的大小是（ ）
A.
B.
C.
D.
【答案】B
【解析】
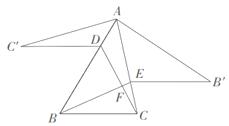
延长C′D交AB′于H．利用全等三角形的性质，平行线的性质，三角形的外角的性质证明∠BFC=∠C′+∠AHC′，再求出∠C′+∠AHC′即可解决问题．
延长C′D交AB′于H．
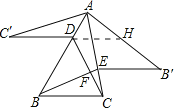
∵△AEB≌△AEB′，
∴∠ABE=∠AB′E，
∵C′H∥EB′，
∴∠AHC′=∠AB′E，
∴∠ABE=∠AHC′，
∵△ADC≌△ADC′，
∴∠C′=∠ACD，
∵∠BFC=∠DBF+∠BDF，∠BDF=∠CAD+∠ACD，
∴∠BFC=∠AHC′+∠C′+∠DAC，
∵∠DAC=∠DAC′=∠CAB′=40°，
∴∠C′AH=120°，
∴∠C′+∠AHC′=60°，
∴∠BFC=60°+40°=100°，
故选：B．
科目：初中数学 来源： 题型：
【题目】已知：如图，折叠矩形ABCD，使点B落在对角线AC上的点F处，若BC＝8，AB＝6，则线段CE的长度是（ ）
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某篮球队对队员进行定点投篮测试，每人每天投篮10次，现对甲、乙两名队员在五天中进球数（单位：个）进行统计，结果如下：
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算，甲进球的平均数为8，方差为3.2.
（1）求乙进球的平均数和方差；
（2）如果综合考虑平均成绩和成绩稳定性两方面的因素，从甲、乙两名队员中选出一人去参加定点投篮比赛，应选谁？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某片果园有果树80棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低，若该果园每棵果树产果y千克，增种果树x棵，它们之间的函数关系如图所示．
(1)求y与x之间的函数解析式；
(2)在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实6750千克？
(3)当增种果树多少棵时，果园的总产量w（千克）最大？最大产量是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从下列算式：①
；②26÷23＝4；③ －12018＝1；④ （－
）2＝3；⑤a＋a＝a2中随机抽取一个，运算结果正确的概率是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明解方程
=3出现了错误，解答过程如下：
方程两边都乘以(x-2)，得1-(1-x)=3(第一步)
去括号，得1-1+x=3(第二步)
移项，合并同类项，得x=3(第三步)
检验，当x=3时x-2≠0(第四步)
所以x=3是原方程的解．(第五步)
(1)小明解答过程是从第____步开始出错的，原方程化为第一步的根据是_____．
(2)请写出此题正确的解答过程．
查看答案和解析>>
科目：初中数学 来源： 题型：
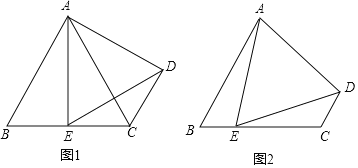
【题目】如图，在四边形ABCD中，AB∥CD，AB＝BC，∠B＝60°，E是BC边上一点．
（1）如图1，若E是BC的中点，∠AED＝60°，求证：CE＝CD；
（2）如图2，若∠EAD＝60°，求证：△AED是等边三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC中，∠C=90°，点P为AC边上的一点，延长BP至点D，使得AD=AP，当AD⊥AB时，过D作DE⊥AC于E，AB-BC=4，AC=8，则△ABP面积为_____
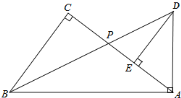
查看答案和解析>>
科目：初中数学 来源： 题型：
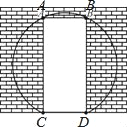
【题目】如图，一面墙上有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接矩形，已知矩形的高AC=2米，宽CD=
米．
(1)求此圆形门洞的半径；
(2)求要打掉墙体的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com