
【题目】如图,已知AB、AC是⊙O的弦,AB、AC的长分别等于⊙O的内接正六边形和正五边形的边长.
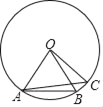
(1)试判断BC的长是否等于⊙O的内接正几边形的边长;
(2)如果⊙O的半径OA=6,求⊙O的内接正六边形的面积.
【答案】(1)BC的长等于⊙O的内接正30边形的边长,理由见解析;
(2)⊙O的内接正六边形的面积为![]() .
.
【解析】
(1)因为AB、AC的长分别等于⊙O的内接正六边形和正五边形的边长,所以∠AOB=60°,∠AOC=72°,即∠BOC=12°,即可得出BC的长等于⊙O的内接正30边形的边长;
(2)先算出△OAB的面积,即可得出⊙O的内接正六边形的面积.
解:(1)∵AB、AC是⊙O的弦,AB、AC的长分别等于⊙O的内接正六边形和正五边形的边长,
∴∠AOB=60°,∠AOC=72°,
∴∠BOC=12°,
∴n=360÷12=30,
∴BC的长等于⊙O的内接正30边形的边长;
(2)∵⊙O的半径OA=6,且△OAB为等边三角形,
∴⊙O的内接正六边形的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】(操作发现)
(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求画图:将ABC绕点A顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,此时∠ABB′等于多少度;
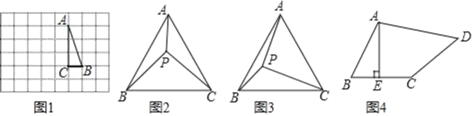
(问题解决)
在某次数学兴趣小组活动中,小明同学遇到了如下问题:
(2)如图2,在等边△ABC中,点P在内部,且PA=3,PC=4,∠APC=150°,求PB的长.
经过同学们的观察、分析、思考、交流、对上述问题形成了如下想法:将△APC绕点A按顺时针方向旋转60°,得到△ABP’,连接PP′,寻找PA、PB、PC三边之间的数量关系……请参考他们的想法,完成该问题的解答过程;
(学以致用)
(3)如图3,在等边△ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°.求△APC的面积;
(思维拓展)
如图4,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k为常数),请直接写出BD的长(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以长为2的线段为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,如图所示.
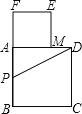
(1)求AM、DM的长;
(2)求证:AM2=ADDM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “任意画一个三角形,其内角和为![]() ”是随机事件;
”是随机事件;
B. 某种彩票的中奖率是![]() ,说明每买100张彩票,一定有1张中奖;
,说明每买100张彩票,一定有1张中奖;
C. “篮球队员在罚球线上投篮一次,投中”为随机事件;
D. 投掷一枚质地均匀的硬币100次,正面向上的次数一定是50次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A在x轴上,点B在第一象限内,∠OAB=90°,OA=AB,△OAB的面积为2,反比例函数y=![]() 的图象经过点B.
的图象经过点B.
(1)求k的值;
(2)已知点P坐标为(a,0),过点P作直线OB的垂线l,点O,A关于直线l的对称点分别为O′,A′,若线段O′A′与反比例函数y=![]() 的图象有公共点,直接写出a的取值范围.
的图象有公共点,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是矩形,AB=2,BC=4,E为BC边上一动点且不与B、C重合,连接AE;
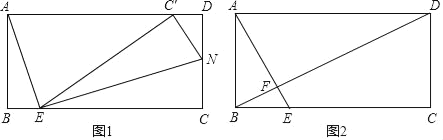
(1)如图1,过点E作EN⊥AE交CD于点N
①若BE=1,求CN的长;②将△ECN沿EN翻折,点C恰好落在边AD上,求BE的长;
(2)如图2,连接BD,设BE=m,试用含m的代数式表示S四边形CDFE:S△ADF值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠ACB=90°,D是BC边上一点,连接AD,分别以CD和AD为直角边作Rt△CDE和Rt△ADF,使∠DCE=∠ADF=90°,点E,F在BC下方,连接EF.
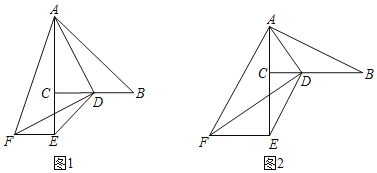
(1)如图1,当BC=AC,CE=CD,DF=AD时,
求证:①∠CAD=∠CDF,
②BD=EF;
(2)如图2,当BC=2AC,CE=2CD,DF=2AD时,猜想BD和EF之间的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点C(0,4),交x轴正半轴于点B,连接AC,点E是线段OB上一动点(不与点O,B重合),以OE为边在x轴上方作正方形OEFG,连接FB,将线段FB绕点F逆时针旋转90°,得到线段FP,过点P作PH∥y轴,PH交抛物线于点H,设点E(a,0).

(1)求抛物线的解析式.
(2)若△AOC与△FEB相似,求a的值.
(3)当PH=2时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com