
ЁОЬтФПЁПЃЈВйзїЗЂЯжЃЉ
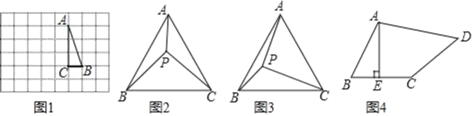
ЃЈ1ЃЉШчЭМ1ЃЌдкБпГЄЮЊ1ИіЕЅЮЛГЄЖШЕФаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌЁїABCЕФШ§ИіЖЅЕуОљдкИёЕуЩЯЃЎЧыАДвЊЧѓЛЭМЃКНЋABCШЦЕуAЫГЪБеыЗНЯђа§зЊ90ЁуЃЌЕуBЕФЖдгІЕуЮЊBЁфЃЌЕуCЕФЖдгІЕуЮЊCЁфЃЌСЌНгBBЁфЃЌДЫЪБЁЯABBЁфЕШгкЖрЩйЖШЃЛ
ЃЈЮЪЬтНтОіЃЉ
дкФГДЮЪ§бЇаЫШЄаЁзщЛюЖЏжаЃЌаЁУїЭЌбЇгіЕНСЫШчЯТЮЪЬтЃК
ЃЈ2ЃЉШчЭМ2ЃЌдкЕШБпЁїABCжаЃЌЕуPдкФкВПЃЌЧвPAЃН3ЃЌPCЃН4ЃЌЁЯAPCЃН150ЁуЃЌЧѓPBЕФГЄЃЎ
ОЙ§ЭЌбЇУЧЕФЙлВьЁЂЗжЮіЁЂЫМПМЁЂНЛСїЁЂЖдЩЯЪіЮЪЬтаЮГЩСЫШчЯТЯыЗЈЃКНЋЁїAPCШЦЕуAАДЫГЪБеыЗНЯђа§зЊ60ЁуЃЌЕУЕНЁїABPЁЏЃЌСЌНгPPЁфЃЌбАевPAЁЂPBЁЂPCШ§БпжЎМфЕФЪ§СПЙиЯЕЁЁЧыВЮПМЫћУЧЕФЯыЗЈЃЌЭъГЩИУЮЪЬтЕФНтД№Й§ГЬЃЛ
ЃЈбЇвджТгУЃЉ
ЃЈ3ЃЉШчЭМ3ЃЌдкЕШБпЁїABCжаЃЌACЃН7ЃЌЕуPдкЁїABCФкЃЌЧвЁЯAPCЃН90ЁуЃЌЁЯBPCЃН120ЁуЃЎЧѓЁїAPCЕФУцЛ§ЃЛ
ЃЈЫМЮЌЭиеЙЃЉ
ШчЭМ4ЃЌдкЫФБпаЮABCDжаЃЌAEЁЭBCЃЌДЙзуЮЊEЃЌЁЯBAEЃНЁЯADCЃЌBEЃНCEЃН1ЃЌCDЃН3ЃЌADЃНkABЃЈkЮЊГЃЪ§ЃЉЃЌЧыжБНгаДГіBDЕФГЄЃЈгУКЌkЕФЪНзгБэЪОЃЉЃЎ
ЁОД№АИЁПЁОВйзїЗЂЯжЁПЃЈ1ЃЉЁЯABЁфBЃН45ЁуЃЛЁОЮЪЬтНтОіЁПЃЈ2ЃЉPBЃН5ЃЛЁОбЇвджТгУЁПЃЈ3ЃЉSЁїAPCЃН7![]() ЃЛЁОЫМЮЌЭиеЙЁПBDЃН
ЃЛЁОЫМЮЌЭиеЙЁПBDЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉСЌНгBBЁфЃЌНЋЁїABCШЦЕуAАДЫГЪБеыЗНЯђа§зЊ90ЁуЃЌдђABЃНABЁфЃЌЁЯBЁфABЃН90ЁуЃЌМДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉгЩЁЯABCЃН60ЁуЃЌНЋЁїAPCШЦЕуAАДЫГЪБеыЗНЯђа§зЊ60ЁуЃЌЕУЕНЁїABP'ЃЌСЌНгPPЁфЃЌдђЁїAPPЁфЪЧЕШБпШ§НЧаЮЃЌЁЯAPCЃНЁЯAPЁфBЃН150ЁуЃЌPCЃНPЁфBЃН4ЃЌЕУГіЁЯAPЁфPЃН60ЁуЃЌPЁфPЃНAPЃН3ЃЌЁЯPPЁфBЃН90ЁуЃЌгЩЙДЙЩЖЈРэМДПЩЕУГіНсЙћЃЛ
ЃЈ3ЃЉНЋЁїAPBШЦЕуAАДФцЪБеыЗНЯђа§зЊ60ЁуЃЌЕУЕНЁїAPЁфCЁфЃЌСЌНгPPЁфЃЌдђЁїAPPЁфЪЧЕШБпШ§НЧаЮЃЌЁЯAPЁфCЃНЁЯAPBЃН360Ёу90Ёу120ЁуЃН150ЁуЃЌЕУГіPPЁфЃНAPЃЌЁЯAPЁфPЃНЁЯAPPЁфЃН60ЁуЃЌЁЯPPЁфCЃН90ЁуЃЌЁЯPЁфPCЃН30ЁуЃЌЭЦГіPPЁфЃН![]() PCЃЌМДAPЃН
PCЃЌМДAPЃН![]() PCЃЌгЩЙДЙЩЖЈРэЕУГіAP2ЃЋPC2ЃНAC2ЃЌМДЃЈ
PCЃЌгЩЙДЙЩЖЈРэЕУГіAP2ЃЋPC2ЃНAC2ЃЌМДЃЈ![]() PCЃЉ2ЃЋPC2ЃН72ЃЌЧѓГіPCЃН2
PCЃЉ2ЃЋPC2ЃН72ЃЌЧѓГіPCЃН2![]() ЃЌAPЃН
ЃЌAPЃН![]() ЃЌгЩШ§НЧаЮУцЛ§ЙЋЪНМДПЩЕУГіНсЙћЃЛ
ЃЌгЩШ§НЧаЮУцЛ§ЙЋЪНМДПЩЕУГіНсЙћЃЛ
ЃЈ4ЃЉгЩЕШбќШ§НЧаЮЕФаджЪЕУГіABЃНACЃЌНЋЁїABDШЦЕуAФцЪБеыа§зЊЕУЕНЁїACGЃЌСЌНгDGЃЎдђBDЃНCGЃЌЕУГіЁЯBACЃНЁЯDAGЃЌЁЯABCЃНЁЯACBЃНЁЯADGЃНЁЯAGDЃЌжЄГіЁїABCЁзЁїADGЃЌЕУГіBCЃН2ЃЌDGЃНkBCЃН2kЃЌжЄЕУЁЯGDCЃН90ЁуЃЌЕУГіCGЃН![]() ЃЌМДПЩЕУГіНсЙћЃЎ
ЃЌМДПЩЕУГіНсЙћЃЎ
НтЃКЃЈ1ЃЉСЌНгBBЁфЃЌНЋЁїABCШЦЕуAАДЫГЪБеыЗНЯђа§зЊ90ЁуЃЌШчЭМ1ЫљЪОЃК

ЁрABЃНABЁфЃЌЁЯBЁфABЃН90ЁуЃЌ
ЁрЁЯABЁфBЃН45ЁуЃЌ
ЙЪД№АИЮЊЃК45ЁуЃЛ
ЃЈ2ЃЉЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯABCЃН60ЁуЃЌ
НЋЁїAPCШЦЕуAАДЫГЪБеыЗНЯђа§зЊ60ЁуЃЌЕУЕНЁїABP'ЃЌСЌНгPPЁфЃЌШчЭМ2ЫљЪОЃК
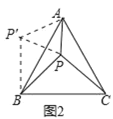
дђЁїAPPЁфЪЧЕШБпШ§НЧаЮЃЌЁЯAPCЃНЁЯAPЁфBЃН150ЁуЃЌPCЃНPЁфBЃН4ЃЌ
ЁрЁЯAPЁфP
ЁрЁЯPPЁфBЃН90ЁуЃЌ
ЁрPBЃН![]() ЃЛ
ЃЛ
ЃЈ3ЃЉНЋЁїAPBШЦЕуAАДФцЪБеыЗНЯђа§зЊ60ЁуЃЌЕУЕНЁїAPЁфCЃЌСЌНгPPЁфЃЌШчЭМ3ЫљЪОЃК
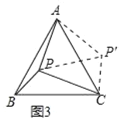
дђЁїAPPЁфЪЧЕШБпШ§НЧаЮЃЌЁЯAPЁфCЃНЁЯAPBЃН360ЁуЉ90ЁуЉ120ЁуЃН150ЁуЃЌ
ЁрPPЁфЃНAPЃЌЁЯAPЁфPЃНЁЯAPPЁфЃН60ЁуЃЌ
ЁрЁЯPPЁфCЃН90ЁуЃЌЁЯPЁфPCЃН30ЁуЃЌ
ЁрPPЁфЃН![]() PCЃЌМДAPЃН
PCЃЌМДAPЃН![]() PCЃЌ
PCЃЌ
ЁпЁЯAPCЃН90ЁуЃЌ
ЁрAP2+PC2ЃНAC2ЃЌМДЃЈ![]() PCЃЉ2+PC2ЃН72ЃЌ
PCЃЉ2+PC2ЃН72ЃЌ
ЁрPCЃН2![]() ЃЌ
ЃЌ
ЁрAPЃН![]() ЃЌ
ЃЌ
ЁрSЁїAPCЃН![]() APPCЃН
APPCЃН![]() ЁС
ЁС![]() ЁС2
ЁС2![]() ЃН7
ЃН7![]() ЃЛ
ЃЛ
(4)ЁпAEЁЭBCЃЌBEЃНECЃЌ
ЁрABЃНACЃЌНЋЁїABDШЦЕуAФцЪБеыа§зЊЕУЕНЁїACGЃЌСЌНгDGЃЎдђBDЃНCGЃЌШчЭМ4ЫљЪОЃК
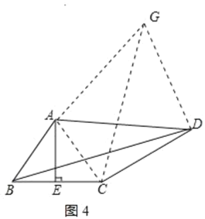
ЁпЁЯBADЃНЁЯCAGЃЌ
ЁрЁЯBACЃНЁЯDAGЃЌ
ЁпABЃНACЃЌADЃНAGЃЌ
ЁрЁЯABCЃНЁЯACBЃНЁЯADGЃНЁЯAGDЃЌ
ЁрЁїABCЁзЁїADGЃЌ
ЁпADЃНkABЃЌBEЃНCEЃН1ЃЌ
ЁрBCЃН2ЃЌDGЃНkBCЃН2kЃЌ
ЁпЁЯBAE+ЁЯABCЃН90ЁуЃЌЁЯBAEЃНЁЯADCЃЌ
ЁрЁЯADG+ЁЯADCЃН90ЁуЃЌ
ЁрЁЯGDCЃН90ЁуЃЌ
ЁрCGЃН![]() ЃЌ
ЃЌ
ЁрDЃНCGЃН![]() ЃЎ
ЃЎ


 ПьРжаЁВЉЪПЙЎЙЬгыЬсИпЯЕСаД№АИ
ПьРжаЁВЉЪПЙЎЙЬгыЬсИпЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУвЛЬѕГЄ40cmЕФЩўзгдѕбљЮЇГЩвЛИіУцЛ§ЮЊ75cm2ЕФОиаЮЃПФмЮЇГЩвЛИіУцЛ§ЮЊ101cm2ЕФОиаЮТ№ЃПШчФмЃЌЫЕУїЮЇЗЈЃЛШчВЛФмЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ;ЕБmЮЊКЮЗЧИКећЪ§ЪБЃК
;ЕБmЮЊКЮЗЧИКећЪ§ЪБЃК
ЃЈ1ЃЉЗНГЬУЛгаЪЕЪ§ИљЃЛЃЈ2ЃЉЗНГЬгаСНИіЯрЕШЕФЪЕЪ§ИљЃЛЃЈ3ЃЉЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЁїABCжаЃЌABЃНACЃЌBCдкжБЯпMNЩЯЃЎ
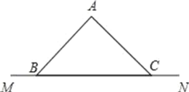
ЃЈ1ЃЉИљОнЯТСавЊЧѓВЙЭъећЭМаЮЃЌ
ЂйЛГіЁїABCЙигкжБЯпMNЖдГЦЕФШ§НЧаЮAЁфBCЃЛ
ЂкдкЯпЖЮBCЩЯШЁСНЕуDЁЂEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЪЙBDЃНCEЃЌСЌНгADЁЂAEЁЂAЁфDЁЂAЁфEЃЛ
ЃЉЃЌЪЙBDЃНCEЃЌСЌНгADЁЂAEЁЂAЁфDЁЂAЁфEЃЛ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮADAЁфEЪЧСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдФГвЛИіКЏЪ§ИјГіШчЯТЖЈвхЃКШчЙћДцдкГЃЪ§![]() ЃЌЖдгкШЮвтЕФКЏЪ§жЕ
ЃЌЖдгкШЮвтЕФКЏЪ§жЕ![]() ЃЌЖМТњзу
ЃЌЖМТњзу![]() Ём
Ём![]() ЃЌФЧУДГЦетИіКЏЪ§ЪЧгаЩЯНчКЏЪ§ЃЛдкЫљгаТњзуЬѕМўЕФ
ЃЌФЧУДГЦетИіКЏЪ§ЪЧгаЩЯНчКЏЪ§ЃЛдкЫљгаТњзуЬѕМўЕФ![]() жаЃЌЦфзюаЁжЕГЦЮЊетИіКЏЪ§ЕФЩЯШЗНчЃЎР§ШчЃЌКЏЪ§
жаЃЌЦфзюаЁжЕГЦЮЊетИіКЏЪ§ЕФЩЯШЗНчЃЎР§ШчЃЌКЏЪ§![]() ЃЌ
ЃЌ ![]() Ём2ЃЌвђДЫЪЧгаЩЯНчКЏЪ§ЃЌЦфЩЯШЗНчЪЧ2ЃЎШчЙћКЏЪ§
Ём2ЃЌвђДЫЪЧгаЩЯНчКЏЪ§ЃЌЦфЩЯШЗНчЪЧ2ЃЎШчЙћКЏЪ§![]() ЃЈ
ЃЈ![]() ЁмxЁм
ЁмxЁм![]() ЃЌ
ЃЌ ![]() ЃМ
ЃМ![]() ЃЉЕФЩЯШЗНчЪЧ
ЃЉЕФЩЯШЗНчЪЧ![]() ЃЌЧветИіКЏЪ§ЕФзюаЁжЕВЛГЌЙ§2
ЃЌЧветИіКЏЪ§ЕФзюаЁжЕВЛГЌЙ§2![]() ЃЌдђ
ЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A. ![]() Ём
Ём![]() B.
B. ![]() C.
C. ![]() Ём
Ём![]() D.
D. ![]() Ём
Ём![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
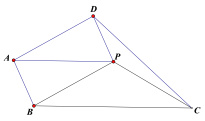
ЁОЬтФПЁПШчЭМЃЌвбжЊPAЃНPBЃНPCЃН4ЃЌЁЯBPCЃН120ЁуЃЌPAЁЮBCЃЌвдABЁЂPBЮЊСкБпзїЦНааЫФБпаЮABPDЃЌСЌНгCDЃЌдђCDЕФГЄЮЊ_____________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
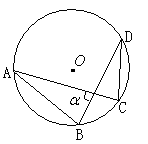
ЁОЬтФПЁПШчЭМЁбOЕФАыОЖЮЊ1cmЃЌЯвABЁЂCDЕФГЄЖШЗжБ№ЮЊ![]() ЃЌдђЯвACЁЂBDЫљМаЕФШёНЧ
ЃЌдђЯвACЁЂBDЫљМаЕФШёНЧ![]() ЃН ЃЎ
ЃН ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгЩ4ИіШЋЕШЕФе§ЗНаЮзщГЩLаЮЭМАИЃЌЧыАДЯТСавЊЧѓЛЭМЃК
(1)дкЭМЂйжаЬэМг1Иіе§ЗНаЮЃЌЪЙЫќГЩжсЖдГЦЭМаЮЃЈВЛФмЪЧжааФЖдГЦЭМаЮЃЉЃЛ
(2)дкЭМЂкжаЬэМг1Иіе§ЗНаЮЃЌЪЙЫќГЩжааФЖдГЦЭМаЮЃЈВЛФмЪЧжсЖдГЦЭМаЮЃЉЃЛ
(3)дкЭМЂлжаИФБф1Иіе§ЗНаЮЕФЮЛжУЃЌДгЖјЕУЕНвЛИіаТЭМаЮЃЌЪЙЫќМШГЩжааФЖдГЦЭМаЮЃЌгжГЩжсЖдГЦЭМаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЁЂACЪЧЁбOЕФЯвЃЌABЁЂACЕФГЄЗжБ№ЕШгкЁбOЕФФкНге§СљБпаЮКЭе§ЮхБпаЮЕФБпГЄЃЎ
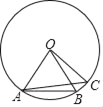
ЃЈ1ЃЉЪдХаЖЯBCЕФГЄЪЧЗёЕШгкЁбOЕФФкНге§МИБпаЮЕФБпГЄЃЛ
ЃЈ2ЃЉШчЙћЁбOЕФАыОЖOAЃН6ЃЌЧѓЁбOЕФФкНге§СљБпаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com