
【题目】问题:如何快速计算1+2+3+…+n 的值呢?
(1)探究:令s=1+2+3+…+n①,则s=n+n-1+…+2+1②
①+②得2s=(n+1)(n+1)+…+(n+1)=n![]() (n+1)
(n+1)
因此![]() _________________.
_________________.
(2)应用:
①计算:![]() ________;
________;
②如图1,一串连续的整数1,2,3,4,…,自上往下排列,最上面一行有一个数,以下各行均比上一行多一个数字,若共有15行数字,则最底下一行最左边的数是_______;
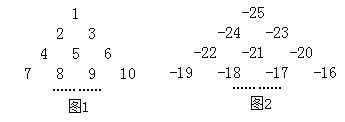
③如图2,一串连续的整数-25,-24,-23,…,按图1方式排列,共有14行数字,求图2中所有数字的和.
科目:初中数学 来源: 题型:
【题目】某商场购进一种单价为40元的书包,如果以单价50元出售,那么每月可售出30个,根据销售经验,售价每提高5元,销售量相应减少1个.
(1)请写出总的销售利润y元与销售单价提高x元之间的函数关系式;
(2)如果你是经理,为使每月的销售利润最大,那么你确定这种书包的单价为多少元?此时,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形![]() 是一个筝形,其中
是一个筝形,其中![]() ,
,![]() ,得到如下结论:①
,得到如下结论:①![]() ;②
;②![]() ;③
;③![]() .④
.④![]() 平分
平分![]() 和
和![]() ;⑤
;⑤![]() 与
与![]() 互相平分,其中正确的结论有(填序号)________.
互相平分,其中正确的结论有(填序号)________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转40°得到△A1BC1,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
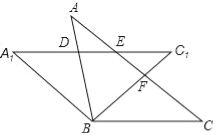
求证:ΔBCF≌ΔBA1D.
当∠C=40°时,请你证明四边形A1BCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
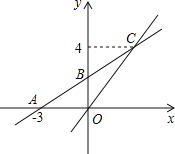
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数![]() 的图象的交于点C(m,4).
的图象的交于点C(m,4).
(1)求m的值及一次函数y=kx+b的表达式;
(2)若点P是y轴上一点,且△BPC的面积为6,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016黑龙江省哈尔滨市)已知:△ABC内接于⊙O,D是![]() 上一点,OD⊥BC,垂足为H.
上一点,OD⊥BC,垂足为H.
(1)如图1,当圆心O在AB边上时,求证:AC=2OH;
(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=∠APB;
(3)在(2)的条件下,如图3,连接BD,E为⊙O上一点,连接DE交BC于点Q、交AB于点N,连接OE,BF为⊙O的弦,BF⊥OE于点R交DE于点G,若∠ACD﹣∠ABD=2∠BDN,AC=![]() ,BN=
,BN=![]() ,tan∠ABC=
,tan∠ABC=![]() ,求BF的长.
,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AF=BD.
(2)求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个边长分别为a,b的正方形.
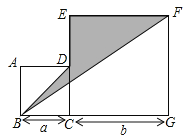
(1)用含a,b的代数式表示三角形BGF的面积;(2)当![]() ,
,![]() 时,求阴影部分的面积.
时,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com