
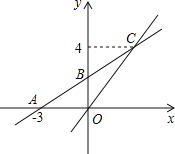
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数![]() 的图象的交于点C(m,4).
的图象的交于点C(m,4).
(1)求m的值及一次函数y=kx+b的表达式;
(2)若点P是y轴上一点,且△BPC的面积为6,请直接写出点P的坐标.
【答案】(1)m的值为3,一次函数的表达式为![]()
(2) 点P 的坐标为(0, 6)、(0,-2)
【解析】
(1)首先利用待定系数法把C(m,4)代入正比例函数y=![]() x中,计算出m的值,进而得到C点坐标,再利用待定系数法A、C两点坐标代入一次函数y=kx+b中,计算出k、b的值进而得到一次函数解析式.
x中,计算出m的值,进而得到C点坐标,再利用待定系数法A、C两点坐标代入一次函数y=kx+b中,计算出k、b的值进而得到一次函数解析式.
(2)利用△BPC的面积为6,即可得出点P的坐标.
解:(1)∵ 点C(m,4)在正比例函数![]() 的图象上,
的图象上,
∴ ![]() ·m,
·m, ![]() 即点C坐标为(3,4)
即点C坐标为(3,4)
∵ 一次函数 ![]() 经过A(-3,0)、点C(3,4)
经过A(-3,0)、点C(3,4)
∴ ![]() 解得:
解得:![]()
∴ 一次函数的表达式为![]()
(2) 点P 的坐标为(0, 6)、(0,-2)
“点睛”此题主要考查了待定系数法求一次函数解析式知识,根据待定系数法把A、C两点坐标代入函数y=kx+b中,计算出k、b的值是解题关键.


科目:初中数学 来源: 题型:
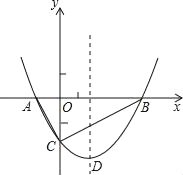
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD交于点O,将一个三角板的直角顶点放置于O处,使其两条直角边分别位于OC的两侧,若OC刚好平分∠BOF,∠BOE=2∠COE,求∠BOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
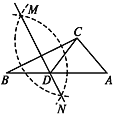
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
A. 90°B. 95°C. 100°D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如何快速计算1+2+3+…+n 的值呢?
(1)探究:令s=1+2+3+…+n①,则s=n+n-1+…+2+1②
①+②得2s=(n+1)(n+1)+…+(n+1)=n![]() (n+1)
(n+1)
因此![]() _________________.
_________________.
(2)应用:
①计算:![]() ________;
________;
②如图1,一串连续的整数1,2,3,4,…,自上往下排列,最上面一行有一个数,以下各行均比上一行多一个数字,若共有15行数字,则最底下一行最左边的数是_______;
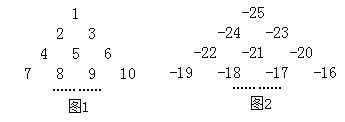
③如图2,一串连续的整数-25,-24,-23,…,按图1方式排列,共有14行数字,求图2中所有数字的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
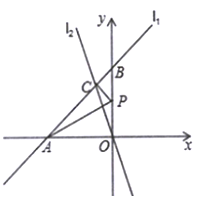
【题目】已知,如图,在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() 两点,直线
两点,直线![]() 过原点且与直线
过原点且与直线![]() 相交于
相交于![]() ,点
,点![]() 为
为![]() 轴上一动点.
轴上一动点.
(1)求点![]() 的坐标;
的坐标;
(2)求出![]() 的面积;
的面积;
(3)当![]() 的值最小时,求此时点
的值最小时,求此时点![]() 的坐标;
的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“双十一”已经成为中国电子商务行业的年度盛事,每年这一天成为全民的购物节.在今年的“双十 一”期间,某网店举办促销活动,方案如下表所示:
一次性购物金额 | 促销方案 |
低于 | 所购商品全部按九折结算 |
| 所购商品全部按八折结算 |
| 其中前 |
![]() 如果顾客在该网店一次性购物
如果顾客在该网店一次性购物![]() 元(
元(![]() ,求实际付款多少元?(用含
,求实际付款多少元?(用含 ![]() 的代数式表示)
的代数式表示)
![]() 某顾客在该店两次购物的商品共计
某顾客在该店两次购物的商品共计![]() 元.若第一次购物商品的金额为
元.若第一次购物商品的金额为 ![]() 元(
元(![]() ),求该顾客两次购物的实际付款共多少元?(用含
),求该顾客两次购物的实际付款共多少元?(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,
,![]() .
.

(1)图中除直角外,还有相等的角吗?请写出两对.
①______②______
(2)如果![]()
①那么根据______可得![]() ______
______
②因为![]() 是
是![]() 的平分线,所以
的平分线,所以![]() ______=______度
______=______度
③求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
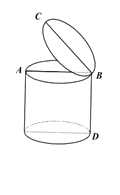
【题目】小明家的脚踏式垃圾桶如图,当脚踩踏板时垃圾桶盖打开最大张角∠ABC =45°,为节省家里空间小明 想把垃圾桶放到桌下,经测量桌子下沿离地面高 55cm,垃圾桶高 BD=33.1cm,桶盖直径 BC=28.2cm,问垃圾桶放到桌下踩踏板时,桶盖完全打开有没有碰到桌子下沿?(![]() 1.41 )
1.41 )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com