
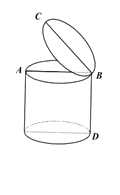
【题目】小明家的脚踏式垃圾桶如图,当脚踩踏板时垃圾桶盖打开最大张角∠ABC =45°,为节省家里空间小明 想把垃圾桶放到桌下,经测量桌子下沿离地面高 55cm,垃圾桶高 BD=33.1cm,桶盖直径 BC=28.2cm,问垃圾桶放到桌下踩踏板时,桶盖完全打开有没有碰到桌子下沿?(![]() 1.41 )
1.41 )

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
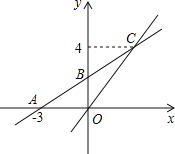
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数![]() 的图象的交于点C(m,4).
的图象的交于点C(m,4).
(1)求m的值及一次函数y=kx+b的表达式;
(2)若点P是y轴上一点,且△BPC的面积为6,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
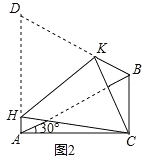
【题目】如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:△AEF≌△BEC;
(2)判断四边形BCFD是何特殊四边形,并说出理由;
(3)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,若BC=1,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)第一版=____%,“第四版”对应扇形的圆心角为________°;
(2)请你补全条形统计图;
(3)若该校有1200名学生,请你估计全校学生中最喜欢“第三版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个边长分别为a,b的正方形.
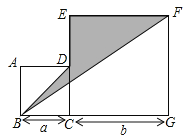
(1)用含a,b的代数式表示三角形BGF的面积;(2)当![]() ,
,![]() 时,求阴影部分的面积.
时,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中两条直线为l1:y=–3x+3,l2:y=–3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:
①a–b+c=0;
②2a+b+c=5;
③抛物线关于直线x=1对称;
④抛物线过点(b,c);
⑤S四边形ABCD=5;
其中正确的个数有( )
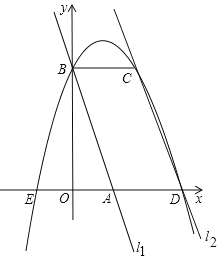
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上.向内放入两个半径为5 cm的钢球,测得上面一个钢球的最高点到底面的距离DC=16 cm(钢管的轴截面如图所示),则钢管的内径AD的长为_______cm.
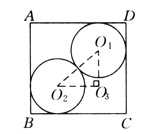
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-1,0),B(1,0),C为y轴正半轴上一点,点D为第三象限一动点,CD交AB于F,且∠ADB=2∠BAC,

(1)求证:∠ADB与∠ACB互补;
(2)求证:CD平分∠ADB;
(3)若在D点运动的过程中,始终有DC=DA+DB,在此过程中,∠BAC的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,AC=8,cosA=![]() ,D是AB边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.
,D是AB边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.
(1)如图1,当DE⊥AC时,求EF的长;
(2)如图2,当点E在AC边上移动时,∠DFE的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出∠DFE的正切值;
(3)如图3,联结CD交EF于点Q,当△CQF是等腰三角形时,请直接写出BF的长.
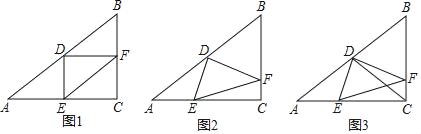
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com