
【题目】如图,已知A(-1,0),B(1,0),C为y轴正半轴上一点,点D为第三象限一动点,CD交AB于F,且∠ADB=2∠BAC,

(1)求证:∠ADB与∠ACB互补;
(2)求证:CD平分∠ADB;
(3)若在D点运动的过程中,始终有DC=DA+DB,在此过程中,∠BAC的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)∠BAC=60°.
【解析】
(1)先判断△ABC是等腰三角形,然后在△ABC中利用三角形内角和定理以及∠ADB=2∠BAC即可得到结论;
(2)过点C作AM⊥DA于点M,作CN⊥BD于点N,运用“AAS”证明△CAM≌△CBN得CM=CN,根据“到角的两边距离相等的点在角的平分线上”得证;
(3)延长DB至点P,使BP=AD,连接CP,则可得CD=DP,证明△CAD≌△CBP,从而可得 △CDP是等边三角形,从而求∠BAC的度数.
(1)∵A(-1,0),B(1,0),
∴OA=OB=1,
∵CO⊥AB,
∴CA=CB,
∴∠ABC=∠BAC,
∵∠ABC+∠BAC+∠ACB=180°,∠ADB=2∠BAC,
∴∠ADB+∠ACB=180°,
即∠ADB与∠ACB互补;
(2)过点C作AM⊥DA于点M,作CN⊥BD于点N,则∠AMC=∠ANB=90°,

∵∠ADB+∠AMC+∠ANB+∠MCN=360°,
∴∠ADB+∠MCN=180°,
又∵∠ADB+∠ACB=180°,
∴∠MCN=∠ACB,
∴∠MCN-∠CAN=∠ACB-∠CAN,
即∠ACM=∠BCN,
又∵AB=AC,
∴△ACM≌△ABN (AAS),
∴AM=AN.
∴CD平分∠ADB(到角的两边距离相等的点在角的平分线上);
(3)∠BAC的度数不变化,
延长DB至点P,使BP=AD,连接CP,

∵CD=AD+BD,
∴CD=DP,
∵∠ADB+∠DBC+∠ACB+∠CAD=360°,∠ADB+∠ACB=180°,
∴∠CAD+∠CBD=180°,
∵∠CBD+∠CBP=180°,
∴∠CAD=∠CBP,
又∵CA=CB,
∴△CAD≌△CBP,
∴CD=CP,
∴CD=DP=CP,即△CDP是等边三角形,
∴∠CDP=60°,
∴∠ADB=2∠CDP=120°,
又∵∠ADB=2∠BAC,
∴∠BAC=60°.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,
,![]() .
.

(1)图中除直角外,还有相等的角吗?请写出两对.
①______②______
(2)如果![]()
①那么根据______可得![]() ______
______
②因为![]() 是
是![]() 的平分线,所以
的平分线,所以![]() ______=______度
______=______度
③求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的脚踏式垃圾桶如图,当脚踩踏板时垃圾桶盖打开最大张角∠ABC =45°,为节省家里空间小明 想把垃圾桶放到桌下,经测量桌子下沿离地面高 55cm,垃圾桶高 BD=33.1cm,桶盖直径 BC=28.2cm,问垃圾桶放到桌下踩踏板时,桶盖完全打开有没有碰到桌子下沿?(![]() 1.41 )
1.41 )

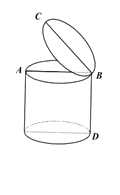
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连结AF、BD.
(1)观察图形,猜想AF与BD之间有怎样的关系,并证明你的猜想;
(2)若将正方形CDEF绕点C按顺时针方向旋转,使正方形CDEF的一边落在△ABC的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然成立?若成立,直接写出结论,不必证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某中学七年级5名学生的体重情况:
姓名 | 小颖 | 小明 | 小刚 | 小京 | 小宁 |
体重(千克) | 34 | 45 | |||
体重与平均体重的差 | -6 | +3 | -4 | 0 |
(1)完成上表.
(2)谁最重?谁最轻?
(3)最重的与最轻的相差多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日,是第23个世界读书日.为了推进中华传统文化教育,营造浓厚的读书氛围,我市某学校举办了“让读书成为习惯,让书香溢病校园”主题活动.为了解学生每周阅读时间,该校随机抽取了部分学生进行调查,根据调查结果,将阅诙时间![]() (单位:小时)分成了
(单位:小时)分成了![]() 组,
组, ![]()
![]()
![]() ,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:
,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:

(1)这次随机抽取了 名学生进行调查;
(2)补全频数分布直方图;
(3)计算扇形统计图中扇形![]() 的圆心角的度数;
的圆心角的度数;
(4)若该校共有![]() 名学生,请你估计每周阅读时间不足
名学生,请你估计每周阅读时间不足![]() 小时的学生共有多少名?
小时的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.

(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6交x轴于A,交y轴于B.

(1)直接写出A( , ),B( , );
(2)如图1,点E为直线y=x+2上一点,点F为直线y=![]() x上一点,若以A,B,E,F为顶点的四边形是平行四边形,求点E,F的坐标
x上一点,若以A,B,E,F为顶点的四边形是平行四边形,求点E,F的坐标
(3)如图2,点C(m,n)为线段AB上一动点,D(﹣7m,0)在x轴上,连接CD,点M为CD的中点,求点M的纵坐标y和横坐标x之间的函数关系式,并直接写出在点C移动过程中点M的运动路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com