
【题目】下表是某中学七年级5名学生的体重情况:
姓名 | 小颖 | 小明 | 小刚 | 小京 | 小宁 |
体重(千克) | 34 | 45 | |||
体重与平均体重的差 | -6 | +3 | -4 | 0 |
(1)完成上表.
(2)谁最重?谁最轻?
(3)最重的与最轻的相差多少?
【答案】(1)答案见解析;(2)小刚的体重最重;小颖的体重最轻;(3)11千克.
【解析】
(1)由小颖的体重与体重和平均体重的差,求出平均体重,进而确定出其他人的体重;
(2)根据表格得出最重、最轻的即可;
(3)用最重的减去最轻的,再进行计算即可.
(1)由小颖体重为34千克,体重与平均体重的差为﹣6,得到平均体重为34﹣(﹣6)=34+6=40(千克),则小明的体重为40+3=43(千克);
小刚的体重与平均体重的差是45﹣40=5千克;
小京的体重为40+(﹣4)=36(千克);
小宁的体重为40千克,填表如下:

(2)小刚的体重最重;小颖的体重最轻.
(3)最重与最轻相差为:45﹣34=11(千克).


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AF=BD.
(2)求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个边长分别为a,b的正方形.
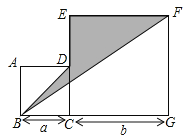
(1)用含a,b的代数式表示三角形BGF的面积;(2)当![]() ,
,![]() 时,求阴影部分的面积.
时,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
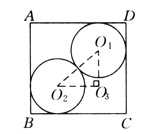
【题目】某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上.向内放入两个半径为5 cm的钢球,测得上面一个钢球的最高点到底面的距离DC=16 cm(钢管的轴截面如图所示),则钢管的内径AD的长为_______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
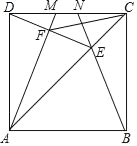
【题目】如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为4,则线段CF的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-1,0),B(1,0),C为y轴正半轴上一点,点D为第三象限一动点,CD交AB于F,且∠ADB=2∠BAC,

(1)求证:∠ADB与∠ACB互补;
(2)求证:CD平分∠ADB;
(3)若在D点运动的过程中,始终有DC=DA+DB,在此过程中,∠BAC的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
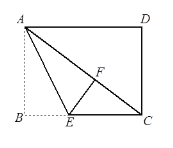
【题目】如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:
①∠BOD=90°;②DO∥AB;③CD=AD;④△BDE∽△BCD;⑤![]()
正确的有( )
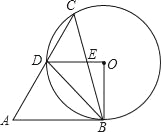
A. ①② B. ①④⑤ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料解决问题:两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,例如37和82,它们各数位上的数字之和分别为3+7和8+2,显然3+7=8+2=10故37和82互为“调和数”.
(1)下列说法错误的是
A.123和51互为调和数” ; B.345和513互为“调和数; C.2018和8120互为“调和数”; D.两位数![]() 和
和![]() 互为“调和数”
互为“调和数”
(2)若A、B是两个不等的两位数,A=![]() ,B=
,B=![]() ,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求证:y=-x+9.
,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求证:y=-x+9.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com