
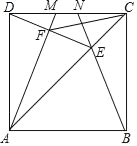
【题目】如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为4,则线段CF的最小值是_____.
【答案】2![]() ﹣2
﹣2
【解析】分析:根据正方形的性质可得AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE,然后利用“HL”证明Rt△ADM和Rt△BCN全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△DCE和△BCE全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AFD=90°,取AD的中点O,连接OF、OC,根据直角三角形斜边上的中线等于斜边的一半可得OF=![]() AD=2,利用勾股定理列式求出OC,然后根据三角形的三边关系可知当O、F、C三点共线时,CF的长度最小.
AD=2,利用勾股定理列式求出OC,然后根据三角形的三边关系可知当O、F、C三点共线时,CF的长度最小.
详解:在正方形ABCD中,AD=BC=CD,∠ADC=∠BCD,∠DCE=∠BCE.在Rt△ADM和Rt△BCN中,![]() ,∴Rt△ADM≌Rt△BCN(HL),∴∠1=∠2.在△DCE和△BCE中,
,∴Rt△ADM≌Rt△BCN(HL),∴∠1=∠2.在△DCE和△BCE中,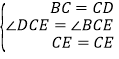 ,∴△DCE≌△BCE(SAS),∴∠2=∠3,∴∠1=∠3.
,∴△DCE≌△BCE(SAS),∴∠2=∠3,∴∠1=∠3.
∵∠ADF+∠3=∠ADC=90°,∴∠1+∠ADF=90°,∴∠AFD=180°﹣90°=90°,取AD的中点O,连接OF、OC,则OF=DO=![]() AD=2.在Rt△ODC中,OC=
AD=2.在Rt△ODC中,OC=![]() =
=![]() =2
=2![]() ,根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=2
,根据三角形的三边关系,OF+CF>OC,∴当O、F、C三点共线时,CF的长度最小,最小值=OC﹣OF=2![]() ﹣2.
﹣2.
故答案为:2![]() ﹣2.
﹣2.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
(1)求证:四边形ABCD是平行四边形;
(2)若AC=2OE,试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
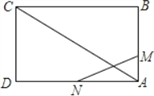
【题目】如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:
(1)经过多少时间,△AMN的面积等于矩形ABCD面积的九分之一?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,猜测MN与BM的数量关系,无需证明.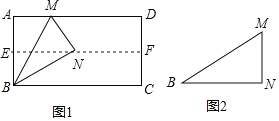
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=![]() 在第一象限内的图象与△ABC有交点,则k的取值范围是_____.
在第一象限内的图象与△ABC有交点,则k的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某中学七年级5名学生的体重情况:
姓名 | 小颖 | 小明 | 小刚 | 小京 | 小宁 |
体重(千克) | 34 | 45 | |||
体重与平均体重的差 | -6 | +3 | -4 | 0 |
(1)完成上表.
(2)谁最重?谁最轻?
(3)最重的与最轻的相差多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组甲队乘一辆汽车沿公路检修线路,约定向东为正,某天从![]() 地出发到收工时,行走记录为(单位:千米):+15、-2、+5、-1、+10、-3、-2、+12、+4、-5、+6;另一小组乙队也从
地出发到收工时,行走记录为(单位:千米):+15、-2、+5、-1、+10、-3、-2、+12、+4、-5、+6;另一小组乙队也从![]() 地出发,在南北方向检修,约定向北为正,行走记录为-17、-9、-2、+8、+6、+9、-5、-1、+4、-7、-8.
地出发,在南北方向检修,约定向北为正,行走记录为-17、-9、-2、+8、+6、+9、-5、-1、+4、-7、-8.
(1)分别计算收工时,两组在![]() 地的哪一边,距
地的哪一边,距![]() 地多远?
地多远?
(2)若每千米汽车耗油量为0.06升,求出发到收工两小组各耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的顶点A,B分别在函数y=-![]() 图象的两个分支上,且AB经过原点O.当点A在函数y=-
图象的两个分支上,且AB经过原点O.当点A在函数y=-![]() 的图象上移动时,顶点C始终在函数y=
的图象上移动时,顶点C始终在函数y=![]() 的图象上移动,则k的值为( )
的图象上移动,则k的值为( )

A. 8B. 6C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
(1)求证:CF=CE
(2)试判断四边形CFHE的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com