
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
(1)求证:CF=CE
(2)试判断四边形CFHE的形状,并说明理由.

【答案】(1)证明见解析;(2)四边形CFHE是菱形.
【解析】
(1)如图,先由直角三角形的性质证∠3=∠5,再由对顶角相等和等量代换得∠4=∠5,从而得到CF=CE;
(2)由角平分线的性质定理得CE=EH,又因为CF=CE,所以CF=EH,再证CF∥EH,得平行四边形CFHE,又因为CF=CE,四边形CFHE是菱形.
(1)证明:如图
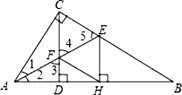
∵∠ACB=90°,CD⊥AB垂足为D,
∴∠1+∠5=90°,∠2+∠3=90°,
又∵∠AE平分∠CAB,
∴∠1=∠2,
∴∠3=∠5,
∵∠3=∠4,
∴∠4=∠5,
∴CF=CE
(2)四边形CFHE是菱形
理由:∵AE平分∠CAB,CE⊥AC,EH⊥AB,
∴CE=EH,
由(1)CF=CE,
∴CF=EH,
∵CD⊥AB,EH⊥AB,
∴∠CDB=90°,∠EHB=90°,
∴∠CDB=∠EB,
∴CD∥EH,即CF∥EH,
∴四边形CFHE是平行四边形.
∵CF=CE,
∴四边形CFHE是菱形.


科目:初中数学 来源: 题型:
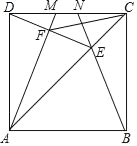
【题目】如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为4,则线段CF的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是在汛期中防汛指挥部对某河流做的一星期的水位测量(单位:![]() )
)
(注:此河流的警戒水位为![]() ,“+”表示比河流的警戒水位高,“-”表示比河流的警戒水位低)
,“+”表示比河流的警戒水位高,“-”表示比河流的警戒水位低)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位记录 | +2.3 | +0.7 | -5.0 | -1.5 | +3.6 | +1.0 | -2.5 |
(1)本周河流水位最高的一天是______,最低的一天是______,这两天的实际水位分别是_______;
(2)完成下列本周的水位变化表(单位:![]() ),(已知上周末河流的水位比警戒水位低
),(已知上周末河流的水位比警戒水位低![]() .注:规定水位比前一天上升用“+”,比前一天下降用“-”,不升不降用“0”)
.注:规定水位比前一天上升用“+”,比前一天下降用“-”,不升不降用“0”)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
(3)与上周末相比,本周末河流水位上升了还是下降了?变化了多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=3,BC=2,沿对角线AC剪开(如图①);固定△ADC,把△ABC沿AD方向平移(如图②),当两个三角形重叠部分的面积最大时,移动的距离AA′等于( )

A. 1 B. 1.5 C. 2 D. 0.8或1.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(0,2![]() ),动点B、C从原点O同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动,以点A为圆心,OB的长为半径画圆;以BC为一边,在x轴上方作等边△BCD.设运动的时间为t秒,当⊙A与△BCD的边BD所在直线相切时,t的值为( )
),动点B、C从原点O同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动,以点A为圆心,OB的长为半径画圆;以BC为一边,在x轴上方作等边△BCD.设运动的时间为t秒,当⊙A与△BCD的边BD所在直线相切时,t的值为( )

A. ![]() B.
B. ![]() C. 4
C. 4![]() +6 D. 4
+6 D. 4![]() -6
-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料解决问题:两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,例如37和82,它们各数位上的数字之和分别为3+7和8+2,显然3+7=8+2=10故37和82互为“调和数”.
(1)下列说法错误的是
A.123和51互为调和数” ; B.345和513互为“调和数; C.2018和8120互为“调和数”; D.两位数![]() 和
和![]() 互为“调和数”
互为“调和数”
(2)若A、B是两个不等的两位数,A=![]() ,B=
,B=![]() ,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求证:y=-x+9.
,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求证:y=-x+9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
(1)求证:四边形ABCD是正方形;
(2)求证:三角形ECF的周长是四边形ABCD周长的一半;
(3)若EC=FC=1,求AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com