
【题目】如图,在矩形纸片ABCD中,AB=3,BC=2,沿对角线AC剪开(如图①);固定△ADC,把△ABC沿AD方向平移(如图②),当两个三角形重叠部分的面积最大时,移动的距离AA′等于( )

A. 1 B. 1.5 C. 2 D. 0.8或1.2
科目:初中数学 来源: 题型:
【题目】(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,猜测MN与BM的数量关系,无需证明.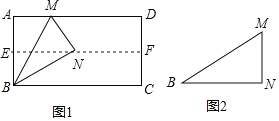
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的顶点A,B分别在函数y=-![]() 图象的两个分支上,且AB经过原点O.当点A在函数y=-
图象的两个分支上,且AB经过原点O.当点A在函数y=-![]() 的图象上移动时,顶点C始终在函数y=
的图象上移动时,顶点C始终在函数y=![]() 的图象上移动,则k的值为( )
的图象上移动,则k的值为( )

A. 8B. 6C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年“绿色清明,文明祭祀”活动中,某花店用![]() 元购进若干菊花,很快售完,接着又用
元购进若干菊花,很快售完,接着又用![]() 元购进第二批菊花,已知第二批所购进菊花的数量是第一批所购进菊花数量的
元购进第二批菊花,已知第二批所购进菊花的数量是第一批所购进菊花数量的![]() 倍,且每朵菊花的进价比第一批每朵菊花的进价多
倍,且每朵菊花的进价比第一批每朵菊花的进价多![]() 元.
元.
(1)求第一批每朵瓶菊花的进价是多少元?
(2)若第一批每朵菊花按![]() 元售价销售,要使总利润不低于
元售价销售,要使总利润不低于![]() 元(不考虑其他因素),第二批每朵菊花的售价至少是多少元?
元(不考虑其他因素),第二批每朵菊花的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 沿
沿![]() 边从点
边从点![]() 开始向终点
开始向终点![]() 以2厘米/秒的速度移动;点
以2厘米/秒的速度移动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向终点
开始向终点![]() 以1厘米/秒的速度移动.如果
以1厘米/秒的速度移动.如果![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间.试解决下列问题:
(秒)表示移动的时间.试解决下列问题:

(1)用含有![]() 、
、![]() 的代数式表示三角形
的代数式表示三角形![]() 的面积;
的面积;
(2)求三角形![]() 的面积(用含有
的面积(用含有![]() 、
、![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
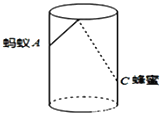
【题目】如图,圆柱形玻璃杯,高为![]() ,底面周长为
,底面周长为![]() ,在杯内离杯底
,在杯内离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿![]() 与蜂蜜相对的点
与蜂蜜相对的点![]() 处,则蚂蚁到达蜂蜜的最短距离为( )
处,则蚂蚁到达蜂蜜的最短距离为( )![]() .
.
A. 15B. ![]() C. 12D. 18
C. 12D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
(1)求证:CF=CE
(2)试判断四边形CFHE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价120元,T恤每件定价60元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款.现某客户要到该服装厂购买夹克30件,T恤![]() 件(
件(![]() >30).
>30).
(1)若该客户按方案①购买,需付款 元(用含x的代数式表示);
若该客户按方案②购买,需付款 元(用含x的代数式表示);
(2)若![]() =40,通过计算说明按方案①、方案②哪种方案购买较为合算?
=40,通过计算说明按方案①、方案②哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当![]() =40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
=40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某房间窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(它们的半径相同):
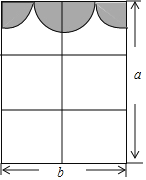
(1)装饰物所占的面积是多少?
(2)窗户中能射进阳光的部分的面积是多少?
(3)计算当a=6,b=4时,窗户中能射进阳光的部分的面积.(π取3.14)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com