
【题目】(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,猜测MN与BM的数量关系,无需证明.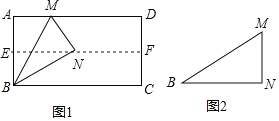
【答案】(1)30,见解析。(2)![]()
【解析】
(1)猜想:∠MBN=30°.如图1中,连接AN.想办法证明△ABN是等边三角形即可解决问题;
(2)MN=![]() BM.折纸方案:如图2中,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.只要证明△MOP≌△BOP,即可解决问题.
BM.折纸方案:如图2中,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.只要证明△MOP≌△BOP,即可解决问题.
(1)猜想:∠MBN=30°.
证明:如图1中,连接AN,∵直线EF是AB的垂直平分线,

∴NA=NB,由折叠可知,BN=AB,
∴AB=BN=AN,
∴△ABN是等边三角形,
∴∠ABN=60°,
∴NBM=∠ABM=![]() ∠ABN=30°.
∠ABN=30°.
(2)结论:MN=![]() BM.
BM.
折纸方案:如图2中,折叠△BMN,使得点N落在BM上O处,
折痕为MP,连接OP.
理由:由折叠可知△MOP≌△MNP,
∴MN=OM,∠OMP=∠NMP=![]() ∠OMN=30°=∠B,
∠OMN=30°=∠B,
∠MOP=∠MNP=90°,
∴∠BOP=∠MOP=90°,
∵OP=OP,
∴△MOP≌△BOP,
∴MO=BO=![]() BM,
BM,
∴MN=![]() BM.
BM.


科目:初中数学 来源: 题型:
【题目】(2016黑龙江省哈尔滨市)已知:△ABC内接于⊙O,D是![]() 上一点,OD⊥BC,垂足为H.
上一点,OD⊥BC,垂足为H.
(1)如图1,当圆心O在AB边上时,求证:AC=2OH;
(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=∠APB;
(3)在(2)的条件下,如图3,连接BD,E为⊙O上一点,连接DE交BC于点Q、交AB于点N,连接OE,BF为⊙O的弦,BF⊥OE于点R交DE于点G,若∠ACD﹣∠ABD=2∠BDN,AC=![]() ,BN=
,BN=![]() ,tan∠ABC=
,tan∠ABC=![]() ,求BF的长.
,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
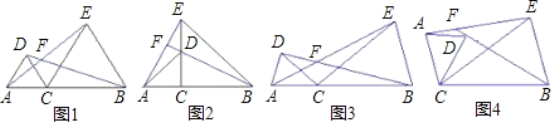
【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB的同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,若∠ACD=60°,则∠AFB=______,如图2,若∠ACD=90°,则∠AFB=______,如图3,若∠ACD=α,则∠AFB=______(用含α的式子表示);
(2)设∠ACD=α,将图3中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),如图4,试探究∠AFB与α的数量关系,并予以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个边长分别为a,b的正方形.
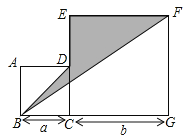
(1)用含a,b的代数式表示三角形BGF的面积;(2)当![]() ,
,![]() 时,求阴影部分的面积.
时,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块三角尺AOB与COD的直角顶点O重合在一起,若∠AOD=4∠BOC,OE为∠BOC的平分线,则∠DOE的度数为( )

A. 36° B. 45° C. 60° D. 72°
查看答案和解析>>
科目:初中数学 来源: 题型:
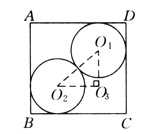
【题目】某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上.向内放入两个半径为5 cm的钢球,测得上面一个钢球的最高点到底面的距离DC=16 cm(钢管的轴截面如图所示),则钢管的内径AD的长为_______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
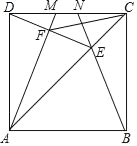
【题目】如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为4,则线段CF的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
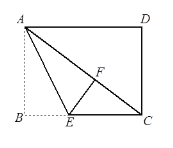
【题目】如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=3,BC=2,沿对角线AC剪开(如图①);固定△ADC,把△ABC沿AD方向平移(如图②),当两个三角形重叠部分的面积最大时,移动的距离AA′等于( )

A. 1 B. 1.5 C. 2 D. 0.8或1.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com