
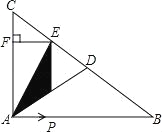
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨°œBAC=90°„£¨AB=4£¨AC=3£¨µ„DŒ™BCµƒ÷–µ„£¨∂ص„P¥”µ„A≥ˆ∑¢£¨“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»—ÿœþ∂ŒABœÚµ„B‘À∂Ø£¨µ±µ„P¿Îø™µ„A∫Û£¨π˝µ„P◊˜PE°ÕABΩªBC”⁄µ„E£¨π˝µ„E◊˜EF°ÕAC”⁄F£¨…˵„P‘À∂Ø ±º‰Œ™t£®√Σ©£¨æÿ–ŒPEFA”ΰ˜ADE÷ÿµ˛≤ø∑÷µƒ√ʪ˝Œ™S∆Ω∑Ωµ•Œª≥§∂»£Æ
£®1£©PEµƒ≥§Œ™ £®”√∫¨tµƒ¥˙ ˝ Ω±Ì æ£©£ª
£®2£©«ÛS”Ît÷ƺ‰µƒ∫Ø ˝±Ì¥Ô Ω£ª
£®3£©«ÛSµƒ◊Ó¥Û÷µº∞S»°µ√◊Ó¥Û÷µ ±tµƒ÷µ£ª
£®4£©µ±SŒ™°˜ABC√ʪ˝µƒ![]() ±£¨tµƒ÷µ”– ∏ˆ£Æ
±£¨tµƒ÷µ”– ∏ˆ£Æ
°æ¥∞∏°ø(1) ![]() £®4-t£©£Æ(2) S=
£®4-t£©£Æ(2) S=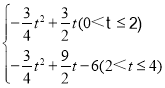 £Æ(3)
£Æ(3) ![]() £Æ(4)4.
£Æ(4)4.
°æΩ‚Œˆ°ø
‘Â∑÷Œˆ£∫£®1£©∏˘æðEP°ŒAC£¨µ√![]() £¨¡–≥ˆ±»¿˝ Ωº¥ø…Ω‚æˆ£Æ
£¨¡–≥ˆ±»¿˝ Ωº¥ø…Ω‚æˆ£Æ
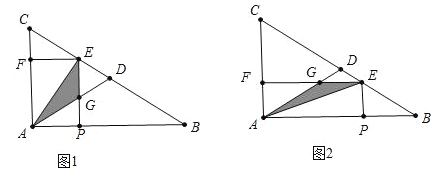
£®2£©∑÷¡Ω÷÷«È–ŒÃ÷¬€¢Ÿ»ÁÕº1÷–£¨µ±0£ºt°Ð2 ±£¨∏˘æðS=![]() EGAPº¥ø…º∆À„£¨¢⁄»ÁÕº2÷–£¨µ±2£ºt°Ð4 ±£¨∏˘æðS=
EGAPº¥ø…º∆À„£¨¢⁄»ÁÕº2÷–£¨µ±2£ºt°Ð4 ±£¨∏˘æðS=![]() GEAFº¥ø…º∆À„£Æ
GEAFº¥ø…º∆À„£Æ
£®3£©∑÷¡Ω÷÷«È–Œ£¨¿˚”√≈‰∑Ω∑®∏˘æð∂˛¥Œ∫Ø ˝–‘÷ º¥ø…Ω‚æˆ£Æ
£®4£©∑÷¡Ω÷÷«È–Œ£¨¡–≥ˆ∑Ω≥ú¥ø…Ω‚æˆ£¨◊¢“‚ºÏ—È «∑Ò∑˚∫œÃ‚“‚£Æ
‘Ã‚Ω‚Œˆ£∫£®1£©»ÁÕº1÷–£¨°þEP°ŒAC£¨
°ý![]() £¨
£¨
°ý![]() ,
,
°ýPE=![]() £®4-t£©£Æ
£®4-t£©£Æ
£®2£©¢Ÿµ±0£ºt°Ð2 ±£¨
°þ°œBAC=90°„£¨CD=DB£¨
°ý°œDAB=°œB£¨°þ°œAPG=°œBAC=90°„£¨
°ý°˜APG°◊°˜BAC£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
°ýPG=![]() t£¨
t£¨
°ýEG=3-![]() t£¨
t£¨
°ýS=![]() EGAP=-
EGAP=-![]() t2+
t2+![]() t£Æ
t£Æ
¢⁄µ±2£ºt°Ð4 ±»ÁÕº2÷–£¨°þ°œFAG=°œC£¨°œAFG=°œBAC£¨
°ý°˜AFG°◊°˜CAB£¨
°ý![]() £¨
£¨
°ýFG=4-t£¨GE=2t-4£¨
°ýS=![]() GEAF=-
GEAF=-![]() t2+
t2+![]() -6£Æ
-6£Æ
◊€…œÀ˘ ˆS=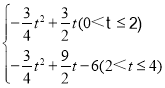 £Æ
£Æ
£®3£©µ±0£ºt°Ð2 ±£¨S=-![]() £®t-1£©2+
£®t-1£©2+![]() £¨
£¨
°þ-![]() £º0£¨
£º0£¨
°ýt=1 ±£¨S◊Ó¥Û÷µŒ™![]() £¨
£¨
µ±2£ºt°Ð4 ±£¨S=-![]() £®t-3£©2+
£®t-3£©2+![]() £¨
£¨
°þ-![]() £º0£¨
£º0£¨
°ýt=3 ±£¨S◊Ó¥Û÷µŒ™![]() £Æ
£Æ
◊€…œÀ˘ ˆt=1ªÚ3 ±£¨S◊Ó¥Û÷µ∂º «![]() £Æ
£Æ
£®4£©”…“‚-![]() t2+
t2+![]() t=
t=![]() £¨’˚¿Ìµ√µΩ5t2-10t+4=0£¨t=
£¨’˚¿Ìµ√µΩ5t2-10t+4=0£¨t=![]() ∑˚∫œÃ‚“‚£Æ
∑˚∫œÃ‚“‚£Æ
ªÚ-![]() t2+
t2+![]() t-6=
t-6=![]() £¨’˚¿Ìµ√µΩ5t2-30t+44=0£¨t=
£¨’˚¿Ìµ√µΩ5t2-30t+44=0£¨t=![]() ∑˚∫œÃ‚“‚£¨
∑˚∫œÃ‚“‚£¨
°ýSŒ™°˜ABC√ʪ˝µƒ![]() ±£¨tµƒ÷µ”–Àƒ∏ˆ£Æ
±£¨tµƒ÷µ”–Àƒ∏ˆ£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∆Ω√ʃ⁄µ„A£®£≠1£¨2£©∫Õµ„B£®£≠1£¨6£©µƒ∂‘≥∆÷· «£® £©
A.x÷·
B.y÷·
C.÷±œþy£Ω4
D.÷±œþx£Ω£≠1
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øµ„Pπÿ”⁄x÷·∂‘≥∆µ„P£ßµƒ◊¯±ÍŒ™£®4£¨£≠5£©£¨ƒ«√¥µ„Pπÿ”⁄y÷·∂‘≥∆µ„P£ß£ßµƒ◊¯±ÍŒ™£® £©
A.£®4£¨5£©
B.£®4£¨£≠5£©
C.£®£≠4£¨5£©
D.£®£≠4£¨£≠5£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬¡–º∆À„’˝»∑µƒ «£®°°°°£©
A. a2+a2£Ωa4B. 3£®a©Åb£©£Ω3a©Åb
C. £®©Åb2£©3£Ω©Åb5D. a2a2£Ωa4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
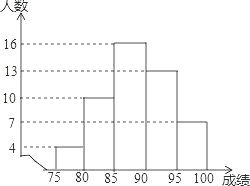
°æƒø°øŒ™¡À¡ÀΩ‚ƒ≥–£»´Ã—߅˙≤Œº”œ˚∑¿÷™ ∂æ∫»¸µƒ≥…º®£®æ˘Œ™’˚ ˝£©£¨¥”÷–≥È»°¡À10%µƒ—ß…˙æ∫»¸≥…º®£¨’˚¿Ì∫ÛªÊ÷∆»Áœ¬µƒ∆µ ˝∑÷≤º÷±∑ΩÕº£¨∆‰÷–£¨√ø◊Èø…∫¨¡ø◊ÓµÕ÷µ£¨≤ª∫¨◊Ó∏þ÷µ£Æ
∏˘æðÕ≥º∆ÕºÃ·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©«Û≤Œº”œ˚∑¿÷™ ∂æ∫»¸µƒ—ß…˙◊лÀ ˝£Æ
£®2£©«Û≥È»°µƒ≤ø∑÷—ß…˙÷–æ∫»¸≥…º®‘⁄85°´90µƒ∆µ¬ £Æ
£®3£©»Áπ˚æ∫»¸≥…º®‘⁄90∑÷“‘…œ£®∫¨90∑÷£©µƒÕ¨—ßø…“‘ªÒµ√Ω±¿¯£¨«Îπ¿º∆∏√–£»´Ã—߅˙÷–ªÒµ√Ω±¿¯µƒ»À ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“ª∏ˆ»˝Ω«–Œµƒ¡Ω±þ≥§∑÷± «2∫Õ7£¨◊Ó≥§±þaŒ™≈º ˝£¨‘Ú’‚∏ˆ»˝Ω«–Œµƒ÷Ð≥§Œ™______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
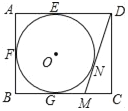
°æƒø°ø»ÁÕº£¨‘⁄æÿ–ŒABCD÷–£¨AB=4£¨AD=5£¨AD£¨AB£¨BC∑÷±”ΰ—Oœý«–”⁄E£¨F£¨G»˝µ„£¨π˝µ„D◊˜°—Oµƒ«–œþBC”⁄µ„M£¨«–µ„Œ™N£¨‘ÚDMµƒ≥§Œ™£® £©
A£Æ![]() B£Æ
B£Æ![]() C£Æ
C£Æ![]() D£Æ
D£Æ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø2016ƒÍƒ˛≤® –±±¬ÿ«¯Ã”˝÷–øºµƒ3∏ˆ—°≤‚œÓƒø∑÷± «50√◊≈У¨“ª∑÷÷”ï…˛£¨¿∫«Ú‘À«ÚÕ∂¿∫£Æ¡ÌπÊ∂®£∫”Œ”æ¬˙∑÷µƒ—ß…˙£¨÷ª–Ë¥”3∏ˆ—°≤‚œÓƒø÷–—°‘Ò“ªœÓΩ¯––≤‚ ‘£ª”Œ”挥µ√¬˙∑÷ªÚŒ¥≤Œº”µƒ—ß…˙£¨–Ë¥”3∏ˆ—°≤‚œÓƒø÷–»Œ—°¡ΩœÓΩ¯––≤‚ ‘£Æ
£®1£©–°√˜“Ú”Œ”æ≤‚ ‘ªÒµ√¡À¬˙∑÷£¨«ÛÀ˚‘⁄3∏ˆ—°≤‚œÓƒø÷–—°‘Ò°∞“ª∑÷÷”ï…˛°±œÓƒøµƒ∏≈¬ £Æ
£®2£©»Ù–°∫Ï∫Õ–°ª€µƒ”Œ”æ≤‚ ‘∂ºŒ¥µ√¬˙∑÷£¨À˝√«∂º±ÿ–Î¥”3∏ˆ—°≤‚œÓƒø÷–—°‘Ò¡ΩœÓΩ¯––Ô˝÷–øº≤‚ ‘£¨«Î”√¡–±Ì£®ªÚª≠ ˜◊¥Õº£©µƒ∑Ω∑®£¨«Û≥ˆ–°∫Ï∫Õ–°ª€—°‘Òµƒ¡Ω∏ˆœÓƒøÕÍ»´œýÕ¨µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com