
����Ŀ��һ��ֱ�����ǰ壨����һ�����ǰ���ڽ���45��,45��,90��,��һ����30��,60��,90����
��1����ͼ�ٷ��ã�AB��AD,��CAE=_______��BC��AD��λ�ù�ϵ��__________��
��2���ڣ�1���Ļ����ϣ�����һ��30��,60��,90���ֱ�����ǰ壬��ͼ�ڷ��ã���AC���ߺ�AD���غϣ� AE�ǡ�CAB���Ľ�ƽ����������ǣ������˵����������ǣ���˵�����ɣ�
��3�����ݣ�1����2���ļ��㣬�����������⣺
��ͼ�ۡ�BAD=90������BAC=��FAD= ![]() ��
��![]() ����ǣ�����һ��45��,45��,90��ֱ�����ǰ��һֱ�DZ���AD���غϣ���Ƕ���A���BAD�Ķ����غϣ�AE�ǡ�CAF�Ľ�ƽ����������ǣ������˵����������ǣ���˵�����ɣ�
����ǣ�����һ��45��,45��,90��ֱ�����ǰ��һֱ�DZ���AD���غϣ���Ƕ���A���BAD�Ķ����غϣ�AE�ǡ�CAF�Ľ�ƽ����������ǣ������˵����������ǣ���˵�����ɣ�

���𰸡�(1)15��,�ƽ�У�(2)����������3��������.
�������������������1����CAE=��BAD����BAC����EAD=15������ΪAB��AD��AB��BC��
����BC��AD�ƽ�У���2���ȼ������EAB��=��EAD����B��AC��=15�����ɣ�1���ɵá�EAB��=��CAE������AE�ǡ�CAB���Ľ�ƽ��������3���ֱ�������CAE=��FAE=45������������AE�ǡ�CAF�Ľ�ƽ���ߣ�
���������
��1����AB��AD��
���BAD=90����
���CAE=90����45����30��=15����
��AB��AD��AB��BC��
��BC��AD�ƽ�У�
��2��AE�ǡ�CAB���Ľ�ƽ���ߣ�
�������£���ͼ�����ߡ�EAD=45������B��AC��=30����
���EAB��=��EAD����B��AC��=15����
���ɣ�1��֪����CAE=15����
���CAE=��EAB������AE�ǡ�CAB���Ľ�ƽ���ߣ�
��3��AE�ǡ�CAF�Ľ�ƽ���ߣ�
�������£���ͼ�����ߡ�EAD=45������BAD=90����
���BAE=��DAE=45����
�֡ߡ�BAC=��FAD=����
���BAE����BAC=��DAE����FAD��
���CAE=��FAE����AE�ǡ�CAF�Ľ�ƽ���ߣ�


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ߵij���2��5�������ߵij��Ƿ���x2��12x+35=0�ĸ���������ߵij�Ϊ��������
A. 2 B. 5 C. 7 D. 5��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η���������֮��Ϊ��3���ǣ� ��
A.x2��3x+3��0B.x2+3x+3��0C.x2+3x��3��0D.x2+6x��4��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������д���ʽ��ֵ
��1����a=-2��b=-3�������ʽ(a+b)2-(a-b)2=___________��
��2����x-y=3ʱ������ʽ2(x-y)2+3x-3y+1=___________.
��3��������ֵ����֪����������![]() �Ļ��Ǹ��������Ϊ��������
�Ļ��Ǹ��������Ϊ��������![]() ʱ�������ʽ
ʱ�������ʽ![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y����x��1��2+2��x������ƽ��2����λ������y������ƽ��3����λ���õ��������߽���ʽΪ��������
A.y����x��3��2+1B.y����x+1��2��1C.y����x��3��2��1D.y����x+1��2��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
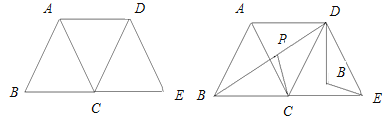
����Ŀ����֪����ȫ�ȵĵȱ���������ͼ1��ʾ���ã����е�B��C��E��ͬһֱ���ϣ�
��1��д��������ͬ���͵Ľ��ۣ�
��2������BD��PΪBD�ϵĶ��㣨D����⣩��DP�Ƶ�D��ʱ����ת60��DQ����ͼ2������PC��QE��
���ж�CP��QE�Ĵ�С��ϵ����˵�����ɣ�
�����ȱ������εı߳�Ϊ2������AP����BD���Ƿ���ڵ�P��ʹAP+CP+DP��ֵ��С��������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P(m��2��m��2)��ƽ��ֱ������ϵ��x���ϣ����P������Ϊ(����)
A. (0����2) B. (2��0) C. (4��0) D. (0����4)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�x-3��(x-2)-p2=0.
��1����֤������pȡ��ֵʱ������������������ȵ�ʵ������
��2���跽����ʵ�����ֱ�Ϊx1��x2��������x12+x22=3 x1x2����ʵ��p��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com