
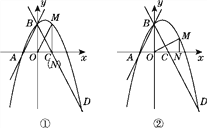
【题目】如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4)
(1)求直线BD和抛物线对应的函数解析式;
(2)在抛物线对称轴上求一点P的坐标,使△ABP的周长最小;
(3)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M,O,N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由.

【答案】(1)y=-2x+2,y=-x2+x+2;(2)(![]() );(3)存在,M(1,2)或
);(3)存在,M(1,2)或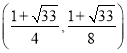 .
.
【解析】试题分析:(1)利用直线与坐标轴的交点坐标,求出抛物线的解析式,利用翻折得出点C的坐标,就可求出直线BD的解析式;(2)本题利用路径最短的知识来解决问题;(3)由(1)的解析式设M(a,-a2+a+2),当△BOC∽△MON或△BOC∽△ONM时,由相似三角形的性质就可以求出结论.
试题解析:(1)易得A(-1,0),B(0,2),C(1,0).
设直线BD对应的函数解析式为y=kx+m.
把B(0,2),C(1,0)的坐标分别代入y=kx+m,
得![]() 解得
解得![]()
∴直线BD对应的函数解析式为y=-2x+2.
∵抛物线对应的函数解析式为y=-x2+bx+c.
∴把B(0,2),D(3,-4)的坐标分别代入y=-x2+bx+c,
得![]() 解得
解得![]()
∴抛物线对应的函数解析式为y=-x2+x+2.
(2)对称轴为:点A(-1,0)关于对称轴的对称点为E(2.0),连接BE交对称轴与点P,则BE的解析式为:y=-x+2 ,当x=![]() 时,BE与对称轴的交点坐标是P:(
时,BE与对称轴的交点坐标是P:(![]() ).
).
(3)存在,①如图①,当△MON∽△BCO时,![]() =
=![]() ,即
,即![]() =
=![]() ,∴MN=2ON.设ON=a,则M(a,2a),∴-a2+a+2=2a,解得a1=-2(不合题意,舍去),a2=1,∴M(1,2);②如图②,当△MON∽△CBO时,
,∴MN=2ON.设ON=a,则M(a,2a),∴-a2+a+2=2a,解得a1=-2(不合题意,舍去),a2=1,∴M(1,2);②如图②,当△MON∽△CBO时,![]() =
=![]() ,即
,即![]() =
=![]() ,∴MN=
,∴MN=![]() ON.设ON=n,则M
ON.设ON=n,则M![]() ,∴-n2+n+2=
,∴-n2+n+2=![]() ,解得n1=
,解得n1=![]() (不合题意,舍去),n2=
(不合题意,舍去),n2=![]() ,∴M(
,∴M(![]() ,
,![]() ).∴存在这样的点M(1,2)或
).∴存在这样的点M(1,2)或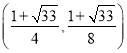 .
.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】下列语句中,是命题的是( )
①两直线平行,同旁内角相等;②π不是有理数;
③同角的余角相等;④明天会下雨吗?⑤延长线段AB.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AD平分∠BAC交BC于点D.
(1)在图1中,将△ABD沿BC的方向平移,使点D移至点C的位置,得到△A′B′D′,且A′B′交AC于点E,猜想∠B′EC与∠A′之间的关系,并说明理由; 
(2)在图2中,将△ABD沿AC的方向平移,使A′B′经过点D,得到△A′B′D′,求证:A′D′平分∠B′A′C. 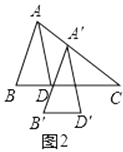
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=![]() 图像的一部分 .其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,
图像的一部分 .其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,![]() ),(
),(![]() ,
,![]() )是抛物线上两点,则
)是抛物线上两点,则![]() >
>![]() 。其中说法正确的是__________(填序号)
。其中说法正确的是__________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器专卖店策划五一促销活动,已知一款电视机的成本价为1800元/台,专卖店计划将其打七五折销售,同时还要保证每台至少获得10%的利润.若设该款电视机的标价为x元/台,则x满足的不等关系为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
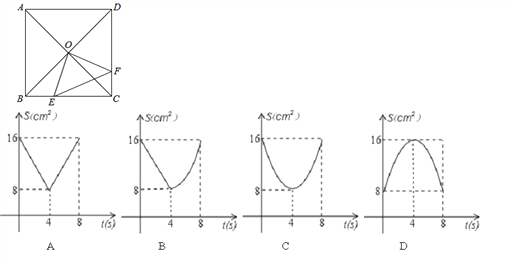
A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com