
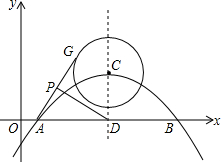
 已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )
已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{{\sqrt{41}}}{2}$ | C. | $\frac{{\sqrt{34}}}{2}$ | D. | $2\sqrt{3}$ |
分析 P为AG中点,D为AB中点,所以PD是三角形ABG的中位线,则DP=1/2 BG,当BG最大时,则DP最大.
由圆的性质可知,当G、C、B三点共线时,BG最大.
解答 解:令$y=-\frac{3}{16}(x-1)(x-9)$=0,得x=1或x=9,
∴A(1,0),B(9,0),
∵$y=-\frac{3}{16}(x-1)(x-9)$=$-\frac{3}{16}(x-5)^{2}+3$,
∴C(5,3),
设P(x,y),
∵P为AG中点,
∴G(2x-1,2y),
∵CG=2,
∴(2x-1-5)2+(2y-3)2=4,
∴${(x-3)}^{2}+(y-\frac{3}{2})^{2}=1$,
即P点在以E(3,$\frac{3}{2}$)为圆心,1为半径的圆上,
∵D(5,0),
∴DE=$\sqrt{(3-5)^{2}+(\frac{3}{2}-0)^{2}}$=$\frac{5}{2}$,
∴DP≤DE+EP=$\frac{5}{2}+1$=$\frac{7}{2}$,
即DP的最大值为$\frac{7}{2}$.
故选A.
点评 本题主要考查了抛物线的交点式和顶点式、圆的定义及基本性质、中点坐标公式、两点间的距离公式、点的轨迹方程、三角形三边关系等知识点,有一定难度.设出P点坐标,求出P点的轨迹方程是解决本题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
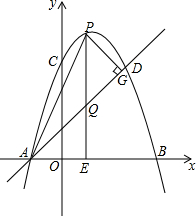 如图,抛物线y=-x2+bx+c 经过A(-1,0),C(0,3)两点,点B是抛物线与x轴的另一个交点,点D与点C关于抛物线对称轴对称,作直线AD.点P在抛物线上,过点P作PE⊥x轴,垂足为点E,交直线AD于点Q,过点P作PG⊥AD,垂足为点G,连接AP.设点P的横坐标为m,PQ的长度为d.
如图,抛物线y=-x2+bx+c 经过A(-1,0),C(0,3)两点,点B是抛物线与x轴的另一个交点,点D与点C关于抛物线对称轴对称,作直线AD.点P在抛物线上,过点P作PE⊥x轴,垂足为点E,交直线AD于点Q,过点P作PG⊥AD,垂足为点G,连接AP.设点P的横坐标为m,PQ的长度为d.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
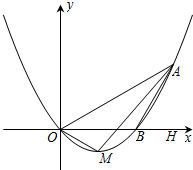 如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AB=BO=2,∠AOB=30°.
如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AB=BO=2,∠AOB=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
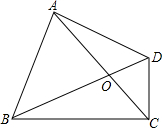 四边形ABCD中,AC、BD相交于点O,∠BAD=90°且AB=AD,CD⊥BC,∠ACB=45°,AC=BC.
四边形ABCD中,AC、BD相交于点O,∠BAD=90°且AB=AD,CD⊥BC,∠ACB=45°,AC=BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com