
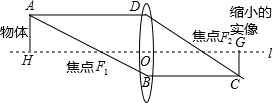
 凸透镜成像的原理如图所示,AD∥l∥BC,若物体到焦点的距离与焦点到凸透镜的中心线DB的距离之比为5:4,则物体被缩小到原来的几分之几?
凸透镜成像的原理如图所示,AD∥l∥BC,若物体到焦点的距离与焦点到凸透镜的中心线DB的距离之比为5:4,则物体被缩小到原来的几分之几?科目:初中数学 来源: 题型:
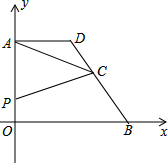 如图,直角坐标系中,0是坐标原点,A,B,C三点的坐标分别是A(0,8),B(10,0),C(7,4),AD∥x轴,与直线BC交于点D,动点P从点A出发,以每秒1个单位的速度,沿折线A-O-B的路线移动,移动的时间是t秒,设△ACP的面积是S.
如图,直角坐标系中,0是坐标原点,A,B,C三点的坐标分别是A(0,8),B(10,0),C(7,4),AD∥x轴,与直线BC交于点D,动点P从点A出发,以每秒1个单位的速度,沿折线A-O-B的路线移动,移动的时间是t秒,设△ACP的面积是S.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
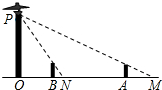 路灯P点距地面9米,身高1.8米的马晓明从距路灯的底部O点20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
路灯P点距地面9米,身高1.8米的马晓明从距路灯的底部O点20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
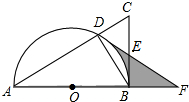 如图,AB是⊙O的直径,点D是半圆圆角上的一点,连结AD,过点B作⊙O的切线BC交AD的延长线于点C,E为BC的中点,连结DE,延长DE交AB的延长线于点F,连接BD.
如图,AB是⊙O的直径,点D是半圆圆角上的一点,连结AD,过点B作⊙O的切线BC交AD的延长线于点C,E为BC的中点,连结DE,延长DE交AB的延长线于点F,连接BD.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| p+q |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com