练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．已知一次函数y=kx+b的图象经过第一、二、三象限，则b的值可以是（　　）
    A．2B．0C．-1D．-2

    分析 根据一次函数图象与系数的关系得到k＞0，b＞0，然后对各选项进行判断．

    解答 解：∵一次函数y=kx+b的图象经过第一、二、三象限，
    ∴k＞0，b＞0，
    ∴b可取2．
    故选A．

    点评 本题考查了一次函数图象与系数的关系：对于一次函数y=kx+b：当k＞0，b＞0?y=kx+b的图象在一、二、三象限；k＞0，b＜0?y=kx+b的图象在一、三、四象限；k＜0，b＞0?y=kx+b的图象在一、二、四象限；k＜0，b＜0?y=kx+b的图象在二、三、四象限．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

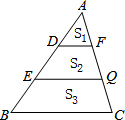    20．如图，在△ABC中，DF∥EQ∥BC，且AD=DE=EB，△ABC被DF、EQ分成三部分，且三部分面积分别为S1，S2，S3，则S1：S2：S3=1：3：5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．（1）计算：$\root{3}{-8}$-（$\frac{1}{2}$）-1+20160；     
    （2）求（x-1）2-25=0中x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

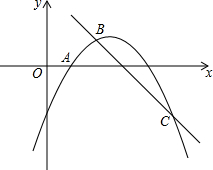    18．如图，在平面直角坐标系xOy中，二次函数y=-$\frac{1}{2}{x^2}$+bx+c的图象经过点A（1，0），且当x=0和x=5时所对应的函数值相等．一次函数y=-x+3与二次函数y=-$\frac{1}{2}{x^2}$+bx+c的图象分别交于B，C两点，点B在第一象限．
    （1）求二次函数y=-$\frac{1}{2}{x^2}$+bx+c的表达式；
    （2）连接AB，求AB的长；
    （3）连接AC，M是线段AC的中点，将点B绕点M旋转180°得到点N，连接AN，CN，判断四边形ABCN的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图：在Rt△ABC中，∠C=90°，BC=8，∠B=60°，解直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

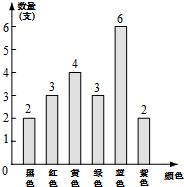    15．有一盒水彩笔除了颜色外无其他差别，其中各种颜色的数量统计如图所示．小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支．小腾抽到蓝色水彩笔的概率为（　　）
    A．$\frac{1}{10}$B．$\frac{1}{5}$C．$\frac{3}{10}$D．$\frac{3}{20}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．老师在课堂上出了一个问题：若点A（-2，y1），B（1，y2）和C（4，y3）都在反比例函数$y=\frac{-8}{x}$的图象上，比较y1，y2，y3的大小．
    小明是这样思考的：当k＜0时，反比例函数的图象是y随x的增大而增大的，并且-2＜1＜4，所以y1＜y2＜y3．
    你认为小明的思考不正确（填“正确”和“不正确”），理由是y2＜y3＜y1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．将二次函数y=x2-2x+3的图象先向上平移2个单位，再向右平移3个单位后，所得新抛物线的顶点坐标为（4，4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．五边形有几条对角线（　　）
    A．14B．16C．9D．5

    查看答案和解析>>

    同步练习册答案