
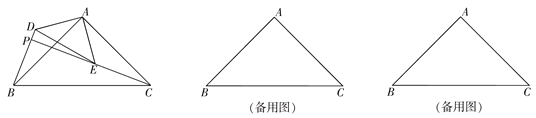
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=![]() ,点P为射线BD,CE的交点.
,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=![]() 时,求PB的长;
时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值.
【答案】(1)详见解析;(2)①![]() 或
或![]() ;②PB长的最小值是
;②PB长的最小值是![]() ,最大值是
,最大值是![]() .
.
【解析】
试题分析:(1)根据已知条件易证△ADB≌△AEC,即可得BD=CE;(2)①分当点E在AB上和当点E在BA延长线上两种情况求PB的长;
试题解析:(1)证明:∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=![]() ,
,
∴AB=AC,AD=AE.
∠DAB=![]() .
.
∴△ADB≌△AEC.
∴BD=CE.
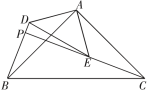
(2)解:①第一种情况:当点E在AB上时,BE=AB-AE=1.
∵∠EAC=![]() ,
,
∴CE=![]() .
.
同(1)可证△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠PEB=∠AEC,
∴△PEB ∽△AEC .
∴![]() . ∴
. ∴![]() .
.
∴![]() .
.
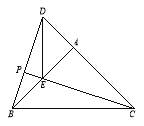
第二种情况:当点E在BA延长线上时,BE=3.
∵∠EAC=![]() ,
,
∴ CE=![]() .
.
同(1)可证△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠BEP=∠CEA,
∴△PEB ∽△AEC .
∴![]() . ∴
. ∴![]() .
.
∴![]() .
.
综上,![]() 或
或![]() .
.
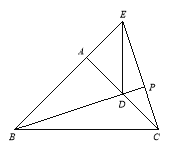
②PB长的最小值是![]() ,最大值是
,最大值是![]() .
.


科目:初中数学 来源: 题型:
【题目】把多项式x2+ax+b分解因式,得(x+1)(x﹣3)则a,b的值分别是( )
A.a=2,b=3
B.a=﹣2,b=﹣3
C.a=﹣2,b=3
D.a=2,b=﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.
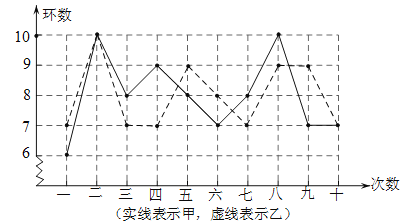
根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动互联网已经全面进入人们的日常生活,截至2016年4月,全国4G用户总数达到1.62亿,其中1.62亿用科学记数法表示为( )
A.1.62×104
B.162×106
C.1.62×108
D.0.162×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
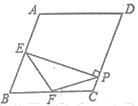
A. 50° B. 55° C. 60° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com