
【题目】(1)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.注意:添加四个符合要求的正方形,并用阴影表示.
(2)先用三角板画∠AOB=60°,∠BOC=45°,然后计算∠AOC的度数.
科目:初中数学 来源: 题型:
【题目】如图,点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA,给出以下结论:①DE平分∠BDC; ②△BCE是等边三角形;③∠AEB=45°;④DE=AD+CD;正确的结论有_____.(请填序号)
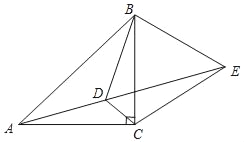
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班师生组织植树活动,上午8时从学校出发,到植树地点植树后原路返校,如图为师生离校路程s与时间t之间的图象.请回答下列问题: 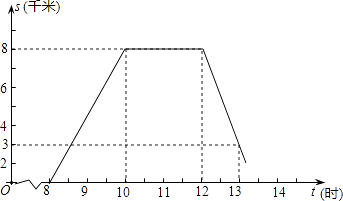
(1)求师生何时回到学校?
(2)如果运送树苗的三轮车比师生迟半小时出发,与师生同路匀速前进,早半小时到达植树地点,请在图中,画出该三轮车运送树苗时,离校路程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
(3)如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
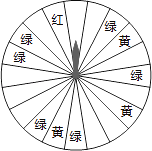
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)点O运动到何处且△ABC满足什么条件时,四边形AECF是正方形?(写出结论即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,下列三角形中,AB=AC,则经过三角形的一个顶点的一条直线 能够将这个三角形分成两个小等腰三角形的是( )
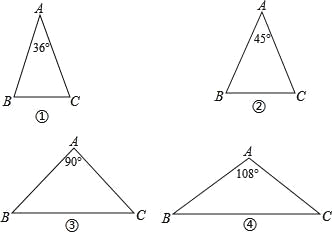
A. ①③④ B. ①②③④ C. ①②④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com