
����Ŀ��2018��11�����쳱ͯʱװ���������山���˰˳��㣬�Ƽ��˰˴�����⳱ͯƷ�ƣ�����Ϊ��Ҵ�����һ��Ʒ������ʢ�ᣬ�������ǽ�Ŀ��ת�Ƶ���00��10��ͯģȺ�����ϣ�������װ���㳱����ij�����̳�ץס����̻�����A��B������ͯװ��1000�����������ۣ�����ÿ��A��ͯװ����160Ԫ��ÿ��B��ͯװ����200Ԫ�������̳�������ÿ��A��ͯװ�����ۼӼ�17Ԫ��ÿ��B��ͯװ�����ۼӼ�15%�������ۣ�ȫ�������꣬������24800Ԫ��
��1����A��B����ͯװ�����ټ���
��2��Ԫ���ڼ���̳��ֹ���A��B����ͯװ���ɼ���չ���˽��۴�������ڴ����ڼ䣬���̳���ÿ��A��ͯװ��������ߣ�m+10��%�������ۣ�ÿ��B��ͯװװ���ۼ۽���![]() m%���ۣ������Ԫ�������ۻ��A��ͯװ���������ȣ�1���е�������������
m%���ۣ������Ԫ�������ۻ��A��ͯװ���������ȣ�1���е�������������![]() m%��B��ͯװ�������ȣ�1����������������20%�������װ��������֮�ͱȣ�1�����������3200Ԫ����m��ֵ��
m%��B��ͯװ�������ȣ�1����������������20%�������װ��������֮�ͱȣ�1�����������3200Ԫ����m��ֵ��
���𰸡���1��A��B����ͯװ��400����600������2��m��ֵ��1��
��������
��1��������������г���Ӧ�ķ��̣��Ӷ����Խ���⣻
��2��������������г���Ӧ�ķ��̣��Ӷ��������m��ֵ��
�⣺��1���蹺��A��ͯװx������B��ͯװ��1000��x������
17x+200��15%����1000��x����24800��
��ã�x��400��
��1000��x��600��
�𣺹���A��B����ͯװ��400����600����
��2��������ɵã�
160����m+10��%��400��1��![]() m%��+[200����1+15%����1��
m%��+[200����1+15%����1��![]() m%����200]��600��1+20%����24800+3200��
m%����200]��600��1+20%����24800+3200��
��ã�m��1��m��0����ȥ����
��m��ֵ��1��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ʶ�ı����ˣ��Ƽ������������������Сѧÿ�궼Ҫ�ٰ�һ��Ƽ��˶��ᣬ��ͼΪ����ijУ����μӿƼ��˶��ẽģ������������ģ����ģ����ģ����ģ�ĸ���𣩵IJ�������ͳ��ͼ��

��1����У�μӳ�ģ����ģ�����������ֱ��� �˺� �ˣ�
��2����У�μӺ�ģ�������������� �ˣ���ģ�������ε�Բ�ĽǵĶ����� ����������ͳ��ͼ����������
��3����ȫ����Сѧ�μӺ�ģ����ѡ���������ȡ80�ˣ�������32�˻�����������Сѧ�μӺ�ģ�����˹���2485�ˣ�����������μӺ�ģ�����Ļ�����Լ�Ƕ����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD����M�DZ�BA�ӳ����ϵĶ��㣨�����A�غϣ�����AM��AB����CBE����DAMƽ�Ƶõ���������E��EH��AC��HΪ���㣬�������½��ۣ�����Mλ�ñ仯��ʹ����DHC=60��ʱ��2BE=DM�������۵�M�˶����δ�������DM=![]() HM�������۵�M�˶����δ�����CHMһ������135�㣮������ȷ���۵����Ϊ_____��
HM�������۵�M�˶����δ�����CHMһ������135�㣮������ȷ���۵����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB���O�����ڵ�C��OA��OB�ֱ�O�ڵ�D,E����CD=��CE��
��1����֤��OA=OB
��2����֪AB=4![]() ��OA=4������Ӱ���ֵ������
��OA=4������Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ө�2����1��3���������������ȡ�������ֱ��Ϊx��y���ѵ�M�������Ϊ��x��y��������NΪ��0��3��������ƽ��ֱ������ϵ��ֱ��MN�����������ĸ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ��һ����Ƶ��ȥ���Ƹ��ʵ�ʵ���У������ijһ������ֵ�Ƶ�ʵ�����ͼ���������һ�����ʵ�������
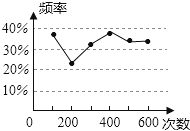
A. ��һö������������ӣ�����1��ĸ���
B. ��һöӲ�ң���������ĸ���
C. ����дһ�����������ܱ�2�����ĸ���
D. ��һ��װ��2�������1������Ĵ�������ȡһ��ȡ������ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() ��������
��������![]() ����
����![]() ��������
��������![]() �����߶�
�����߶�![]() Ϊֱ������
Ϊֱ������![]() ����
����![]() ����������ڵ�
����������ڵ�![]() ����
����![]() ��
��![]() ��
��![]() �����������ߣ�
�����������ߣ�
��1���������ߵĽ���ʽ��
��2������![]() ��
��![]() ����
����![]() ��
��![]() �ӳ�����һ�㣬
�ӳ�����һ�㣬![]() �Ľ�ƽ����
�Ľ�ƽ����![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ����ֱ��
����ֱ��![]() ����һ��
����һ��![]() ��ʹ��
��ʹ��![]() ���ܳ���С���������ʱ��
���ܳ���С���������ʱ��![]() �����ꣻ
�����ꣻ
��3���ڣ�2���������£����������Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ���ֱ��д����
�������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����OA=OB��
��1����֤���ı���ABCD�Ǿ��Σ�
��2����AB=2����AOB=60������BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB�������ߵĽ�����A(0��-3)��B(5��9)����֪�����ߵĶ���D�ĺ�������2.

(1)�������ߵĽ���ʽ���������ꣻ
(2)��![]() �����Ƿ����һ��C����A��B��ɵ��������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
�����Ƿ����һ��C����A��B��ɵ��������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
(3)��ֱ��AB���·�����������һ��P������PA��PBʹ�á�PAB�����������������ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com