问题提出：从A到B共有8个台阶，如果某同学在上台阶时，可以一步1个台阶，也可以一步2个台阶．那么该同学从A走到B共有多少种不同的走法？
问题探究：为解决上述实际问题，我们先建立如下数学模型：
用若干个边长都为1的正方形（记为1×1矩形）和若干个边长分别为1和2的矩形（记为1×2矩形），如图1，要拼成一个边长分别为1和n的矩形（记为1×n矩形），如图2，有多少种不同的拼法？（设A
1×n表示不同拼法的个数）
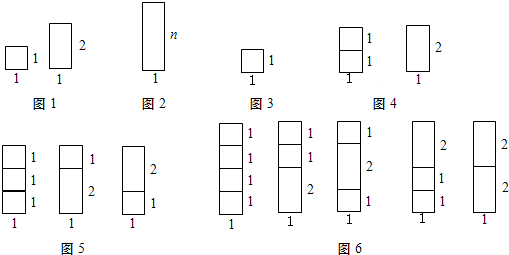
为解决上述数学模型问题，我们采取的策略和方法是：一般问题特殊化．
探究一：先从最特殊的情形入手，即要拼成一个1×1矩形，有多少种不同拼法？
显然，只有1种拼法，如图3，即A
1×1=1种．
探究二：要拼成一个1×2矩形，有多少种不同拼法？不难看出，有2种拼法，如图4，即A
1×2=2种．
探究三：要拼成一个1×3矩形，有多少种不同拼法？拼图方法可分为两类：一类是在图4这2种1×2矩形
上方，各拼上一个1×1矩形，即这类拼法共有A
1×2=2种；另一类是在图3这1种1×1矩形上方拼上一个1×2矩形，即这类拼法有A
1×1=1种，如图5．即A
1×3=A
1×2+A
1×1=2+1=3（种）．
探究四：要拼成一个1×4矩形，有多少种不同拼法？拼图方法可分为两类：一类是在图5这3种1×3矩形上方，各拼上一个1×1矩形，即这类拼法共有A
1×3=3种；另一类是在图4这2种1×2矩形上方，各拼上一个1×2矩形，即这类拼法共有A
1×2=2种，如图6．即A
1×4=A
1×3+A
1×2=3+2=5（种）．
探究五：要拼成一个1×5矩形，有多少种不同拼法A
1×5？仿照上述探究过程进行解答，并求出A
1×5（不需画图）．
探究六：一般的，要拼成一个1×n矩形（n≥3的整数），有A
1×n=
种不同拼法．（已知A
1×（n-1）=a，A
1×（n-2）=b，）
问题解决：把“问题提出”中的实际问题，转化为“问题探究”中的数学模型，并进行解答．
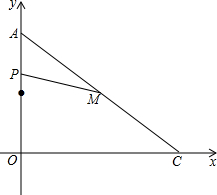如图，在平面直角坐标系中，A（0，6），C（8，0），点M是AC的中点，点P从点A出发，沿着AO→OC的折线运动到C点停止．当以点A，M，P为顶点的三角形是等腰三角形时，直接写出点P的坐标，并写出相应的tan∠APM的值．
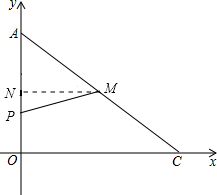分三种情况：
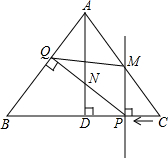已知，如图，在△ABC中，AB=AC=10cm，BC=12cm，AD⊥BC于D，直线PM从点C出发沿CB方向匀速运动，速度为1cm/s；运动过程中始终保持PM⊥BC，直线PM交BC于P，交AC于点M；过点P作PQ⊥AB，交AB于Q，交AD于点N，连接QM，设运动时间是t（s）（0＜t＜6），解答下列问题：
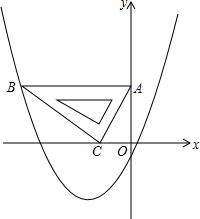在平面直角坐标系中，现将一块含30°的直角三角板ABC放在第二象限，30°角所对的直角边AC斜靠在两坐标轴上，且点A（0，3），点C（-