
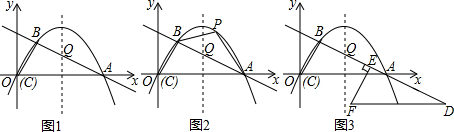
分析 (1)作BG⊥x轴于点G,证得△ABC∽△BGC后利用相似三角形对应边的比相等AC=10,从而确定点A的坐标,利用待定系数法确定二次函数的解析式即可;
(2)连接PG,设点P(m,-$\frac{1}{4}$m2+$\frac{5}{2}$m),利用S=S△BPG+S△APG-S△ABG得到当m=6时,△ABP的面积有最大值,S最大=16,从而求得P(6,6);
(3)首先得到直线L的解析式为y=-$\frac{1}{2}$x,然后设F(n,-$\frac{1}{2}$n),分①点F为顶点、②点A为顶点、③点Q为顶点三种情况分别求得F点的坐标即可;
解答 解:(1)如图所示,作BG⊥x轴于点G,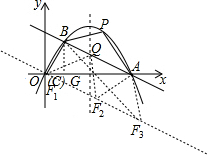
∵B(2,4),
∴CG=2,BG=4,
∴BC=$\sqrt{O{G}^{2}+B{G}^{2}}$=2$\sqrt{5}$,
∵∠CBA=90°,
∴△ABC∽△BGC,
∴$\frac{BC}{AC}=\frac{CG}{BC}$;
即:$\frac{2\sqrt{5}}{AC}=\frac{2}{2\sqrt{5}}$,
解得:AC=10,
∴A(10,0),
∴抛物线经过A,B,C三点,点C为原点,
∴设抛物线的解析式为y=ax2+bx,
将A、B点的坐标分别代入得:
$\left\{\begin{array}{l}{100a+10b=0}\\{4a+2b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{5}{2}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{4}$x2+$\frac{5}{2}$x=-$\frac{1}{4}$(x-5)2+$\frac{25}{4}$;
(2)如图所示,连接PG,设点P(m,-$\frac{1}{4}$m2+$\frac{5}{2}$m),
则S=S△BPG+S△APG-S△ABG
=$\frac{1}{2}$BG•|xP-xB|+$\frac{1}{2}$×8×(-$\frac{1}{4}$m2+$\frac{5}{2}$m)-$\frac{1}{2}$AG•BG
=$\frac{1}{2}$×4×(m-2)+$\frac{1}{2}$×8×(-$\frac{1}{4}$m2+$\frac{5}{2}$m)-$\frac{1}{2}$×4×8
=-m2+12m-20
=-(m-6)2+16,
∴当m=6时,△ABP的面积有最大值,S最大=16,
∴-$\frac{1}{4}$×62+$\frac{5}{2}$×6=6,
∴P(6,6);
(3)由(1)可知抛物线的对称轴为x=5,
由A,B两点坐标可求得直线AB的解析式为y=-$\frac{1}{2}$x+5,
将x=5代入,解得:y=$\frac{5}{2}$,
∴Q(5,$\frac{5}{2}$)
∴AQ=$\sqrt{(10-5)^{2}+(0-\frac{5}{2})^{2}}$=$\frac{5}{2}\sqrt{5}$.
∵△ABC沿BA平移,得△DEF,
∴点F在过原点且平行于AB的直线上,
∴直线L的解析式为y=-$\frac{1}{2}$x,
∴设F(n,-$\frac{1}{2}$n),
①若点F为等腰三角形的顶点,则QF=AF,
即(n-5)2+(-$\frac{1}{2}$n-$\frac{5}{2}$)2=(n-10)2+(0+$\frac{1}{2}$n)2,
解得:n=$\frac{11}{2}$,
∴F1($\frac{11}{2}$,-$\frac{11}{4}$);
②若点A为等腰三角形的顶点,则AF=AQ.
∴$\sqrt{(n-10)^{2}+(-\frac{1}{2}n-0)^{2}}$=$\frac{5}{2}\sqrt{5}$
整理得:n2-16n+55=0
解得:n=11或n=5
∴F2(11,-$\frac{11}{2}$),F3(5,-$\frac{5}{2}$);
③若点Q为等腰三角形的顶点,则QF=QA.
∴$\sqrt{{(n-5)}^{2}+{(-\frac{1}{2}n-\frac{5}{2})}^{2}}$=$\frac{5}{2}\sqrt{5}$
整理得:n2-6n=0
解得:n=0(舍去)或n=6
∴F4(6,-3).
综上所述,满足题意的点F有4个,分别为:F1($\frac{11}{2}$,-$\frac{11}{4}$),F2(11,-$\frac{11}{2}$),F3(5,-$\frac{5}{2}$),F4(6,-3).
点评 本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 计算日期 | 上期示度 | 本期示度 | 电量 | 金额(元) |
| 20110710 | 3 230 | 3 296 | 66 | 34.98 |
| 20110810 | 3 296 | 3 535 | 239 | 135.07 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
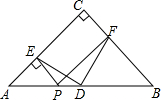 △ABC中,∠C=90°,BC=AC,D为AB中点,P是AB上一点,PE⊥AC于E,PF⊥BC于F.
△ABC中,∠C=90°,BC=AC,D为AB中点,P是AB上一点,PE⊥AC于E,PF⊥BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com