
分析 (1)根据负整数指数幂、零指数幂的二次根式计算即可;
(2)根据分式的加减进行计算;
(3)根据分式的加减进行计算;
(4)先化简,再代入数值解答即可.
解答 解:(1))${({\frac{1}{2}})^{-2}}-\sqrt{12}-{({\sqrt{3}-2})^0}$
=4-2$\sqrt{3}$-1
=3-2$\sqrt{3}$;
(2)$\frac{m-15}{{{m^2}-9}}-\frac{2}{3-m}$
=$\frac{m-15}{{m}^{2}-9}+\frac{2(m+3)}{{m}^{2}-9}$
=$\frac{m-15+2m+6}{{m}^{2}-9}$
=$\frac{3m-9}{{m}^{2}-9}$
=$\frac{3}{m+3}$;
(3)$\frac{a^2}{a+b}-a+b$
=$\frac{{a}^{2}-a(a+b)+b(a+b)}{a+b}$
=$\frac{{a}^{2}-{a}^{2}-ab+ab+{b}^{2}}{a+b}$
=$\frac{{b}^{2}}{a+b}$;
(4)$\frac{a-b}{a}÷(a-\frac{2ab-{b}^{2}}{a})$
=$\frac{a-b}{a}÷(\frac{{a}^{2}-2ab+{b}^{2}}{a})$
=$\frac{a-b}{a}×\frac{a}{(a-b)^{2}}$
=$\frac{1}{a-b}$;
把a=2,b=1代入原式=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:填空题
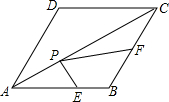 如图,在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE+PF的最小值是5$\sqrt{3}$.
如图,在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE+PF的最小值是5$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
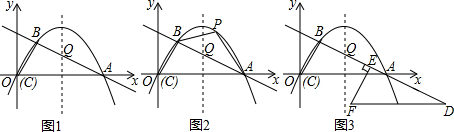
 甲从M地出发去N地,乙搭甲的便车也从M地出发到途中与M,N两地在同一条直线上的G地.甲在N地停留一段时间后以110km/h的速度返回,乙在G地停留了$\frac{3}{4}$h后,徒步返回M地,走了5km时与返回的甲相遇并搭甲车返回M地.如图是两人与M地的距离y(单位:km)与行进时间x(单位:h)之间的函数图象(甲、乙均匀速行进,不考虑其他因素).
甲从M地出发去N地,乙搭甲的便车也从M地出发到途中与M,N两地在同一条直线上的G地.甲在N地停留一段时间后以110km/h的速度返回,乙在G地停留了$\frac{3}{4}$h后,徒步返回M地,走了5km时与返回的甲相遇并搭甲车返回M地.如图是两人与M地的距离y(单位:km)与行进时间x(单位:h)之间的函数图象(甲、乙均匀速行进,不考虑其他因素).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
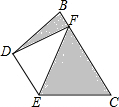 DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )
DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com