
【题目】铜仁市积极推动某公园建设,通过旅游带动一方经济,计划经过若干年使公园绿化总面积新增450万平方米.自2016年初开始实施后,实际每年绿化面积是原计划的1.5倍,这样可以提前3年完成任务.
(1)求实际每年绿化面积是多少万平方米
(2)为加大公园绿化力度,市政府决定从2019年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
【答案】(1)实际每年绿化面积为75万平方米;(2)平均每年绿化面积至少还要增加37.5万平方米.
【解析】
(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.5x万平方米.根据“实际每年绿化面积是原计划的1.5倍,这样可提前3年完成任务”列出方程;
(2)设平均每年绿化面积增加a万平方米.则由“完成新增绿化面积不超过2年”列出不等式.
解:(1)设原计划每年绿化面积为x万平方米,
![]() ,
,
解得x=50,
经检验,x=50是此分式方程的解.
∴1.5x=75.
答:实际每年绿化面积为75万平方米.
(2)设平均每年绿化面积至少还要增加a万平方米,
75×3+2(75+a)≥450,解得a≥37.5.
答:平均每年绿化面积至少还要增加37.5万平方米.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
阅读理解:数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用较大数与较小数的差来表示.例如:
在数轴上,有理数3与1对应的两点之间的距离为![]() ;
;
在数轴上,有理数3与-2对应的两点之间的距离为![]() ;
;
在数轴上,有理数-3与-2对应的两点之间的距离为![]() .
.
解决问题:如图所示,已知点![]() 表示的数为-3,点
表示的数为-3,点![]() 表示的数为-1,点
表示的数为-1,点![]() 表示的数为2.
表示的数为2.
![]()
(1)点![]() 和点
和点![]() 之间的距离为______.
之间的距离为______.
(2)若数轴上动点![]() 表示的数为
表示的数为![]() ,当
,当![]() 时,点
时,点![]() 和点
和点![]() 之间的距离可表示为______;当
之间的距离可表示为______;当![]() 时,点
时,点![]() 和点
和点![]() 之间的距离可表示为______.
之间的距离可表示为______.
(3)若数轴上动点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在点
在点![]() 和点
和点![]() 之间,点
之间,点![]() 和点
和点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 和点
和点![]() 之间的距离表示为
之间的距离表示为![]() ,求
,求![]() (用含
(用含![]() 的代数式表示并进行化简)
的代数式表示并进行化简)
(4)若数轴上动点![]() 表示的数为-2,将点
表示的数为-2,将点![]() 向右移动19个单位长度,再向左移动23个单位长度终点为
向右移动19个单位长度,再向左移动23个单位长度终点为![]() ,那么
,那么![]() ,
,![]() 两点之间的距离是______.
两点之间的距离是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
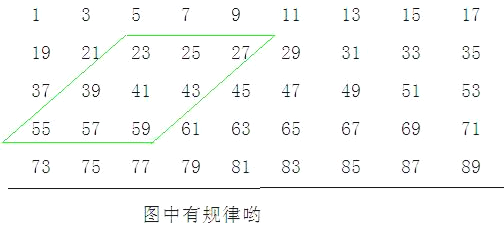
【题目】下图的数阵是由全体奇数排成:
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个;若不能,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为4的正方形ABCD,顶点A与坐标原点重合,一反比例函数图象过顶点C,动点P以每秒1个单位速度从点A出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
(1)求出该反比例函数解析式;
(2)连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标;
(3)用含t的代数式表示以点Q、P、D为顶点的三角形的面积s,并指出相应t的取值.

查看答案和解析>>
科目:初中数学 来源: 题型:
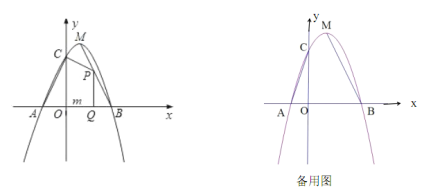
【题目】如图,已知二次函数![]() (
(![]() )的图象与
)的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() ,顶点为
,顶点为![]() .
.
(1)求二次函数的解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)探索:线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形?如果存在,求出点
为直角三角形?如果存在,求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
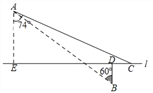
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com