
【题目】某商店经销一种小家电,每个小家电的成本为20元,市场调查发现,该种小家电每天的销售量y(个)与销售单价x(元)的函数图象如图.设这种小家电每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)如果物价部门规定这种小家电的销售单价不高于32元,该商店销售这种小家电每天要获得400元的销售利润,销售单价应定为多少元?
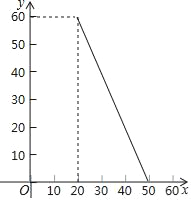
【答案】(1)w=﹣2x2+140x﹣2000;(2)该商店销售这种小家电每天要获得400元的销售利润,销售单价应定为30元.
【解析】试题分析:(1)先求得销售量y(个)与销售单价x(元)的函数关系式,再根据“利润=销售量×(销售单价-成本)”即可得;
(2)将w=400代入(1)中的关系式,解方程后进行比较即可得.
试题解析:(1)设y=kx+b,
则![]() ,
,
解得: ![]() ,
,
则y=﹣2x+100(20≤x≤50),
所以w=(x﹣20)(﹣2x+100)=﹣2x2+140x﹣2000;
(2)根据题意,得:﹣2x2+140x﹣2000=400,
解得:x=30或x=40,
因为x≤32,
所以x=30,
答:该商店销售这种小家电每天要获得400元的销售利润,销售单价应定为30元.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】近年来,手机微信红包迅速流行起来.去年春节,小米的爷爷也尝试用微信发红包,他分别将10元、30元、60元的三个红包发到只有爷爷、爸爸、妈妈和小米的微信群里,他们每人只能抢一个红包,且抢到任何一个红包的机会均等(爷爷只发不抢,红包里钱的多少与抢红包的先后顺序无关).
(1)求小米抢到60元红包的概率;
(2)如果小米的奶奶也加入“抢红包”的微信群,他们四个人中将有一个人抢不到红包,那么这种情况下,求小米和妈妈两个人抢到红包的钱数之和不少于70元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
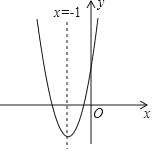
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c; ④4a﹣2b+c>0,其中正确有_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是一位同学所做的有理数运算解题过程的一部分:
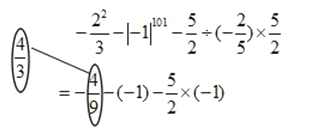
(1)请你在上面的解题过程中仿照给出的方式,圈画出他的错误之处,并将正确结果写在相应的圈内;
(2)请就此题反映出的该同学有理数运算掌握的情况进行具体评价,并对相应的有效避错方法给出你的建议。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形 ABCD 中,动点 E 从点 A 出发,沿 AB→BC 方向运动,当点 E 到达点 C 时 停止运动.过点 E 作 FE⊥AE,交 CD 于 F 点,设点 E 运动路程为 x,FC=y,图②表示 y与 x 的函数关系的大致图像,则矩形 ABCD 的面积是( )

A. ![]() B. 5 C. 6 D.
B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用5个棱长为1的正方体组成如图所示的几何体.
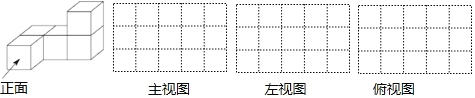
(1)该几何体的体积是多少立方单位,表面积是多少平方单位(包括底面积);
(2)请在方格纸中用实线画出它的三个视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
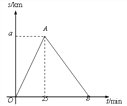
【题目】某市举行长跑比赛,运动员从甲地出发跑到乙地后,又沿原路线跑回起点甲地.如图是某运 动员离开甲地的路程 s(km)与跑步时间 t(min)之间的函数关系(OA、OB 均为线段).已 知该运动员从甲地跑到乙地时的平均速度是 0.2 km/min,根据图像提供的信息,解答下列问 题:
(1)a= km;
(2)组委会在距离起点甲地 3 km 处设立了一个拍摄点 P,该运动员从第一次过 P 点到第二
次过 P 点所用的时间为 24 min.
①求 AB 所在直线的函数表达式;
②该运动员跑完全程用时多少 min?
查看答案和解析>>
科目:初中数学 来源: 题型:
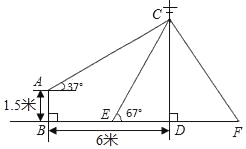
【题目】如图,在电线杆CD处引拉线CE,CF固定电线杆,拉线CE和地面所成的角∠CED=67°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为37°,求拉线CE的长(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tsn37°≈
,tsn37°≈![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com