
【题目】如图,小明在山脚下的A处测得山顶N的仰角为45°,此时,他刚好与山底D在同一水平线上.然后沿着坡度为30°的斜坡正对着山顶前行110米到达B处,测得山顶N的仰角为60°.求山的高度.(结果精确到1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732).
≈1.732).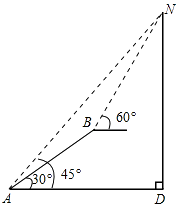
【答案】解:过点B作BF⊥DN于点F,过点B作BE⊥AD于点E,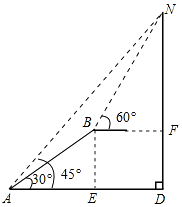
∵∠D=90°,
∴四边形BEDF是矩形,
∴BE=DF,BF=DE,
在Rt△ABE中,AE=ABcos30°=110× ![]() =55
=55 ![]() (米),
(米),
BE=ABsin30°= ![]() ×110=55(米),
×110=55(米),
设BF=x米,则AD=AE+ED=55 ![]() +x(米),
+x(米),
在Rt△BFN中,NF=BFtan60°= ![]() x(米),
x(米),
∵∠NAD=45°,
∴AD=DN,
∴DN=DF+NF=55+ ![]() x(米),
x(米),
即55 ![]() +x=
+x= ![]() x+55,
x+55,
解得:x=55,
∴DN=55+ ![]() x≈150(米),
x≈150(米),
答:山的高度约为150米.
【解析】过点B作BF⊥DN于点F,过点B作BE⊥AD于点E,根据余弦的定义求出AE,根据正弦的定义求出BE,设BF=x米,根据正切的定义求出NF,结合图形列出方程,解方程即可.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AB的中点,DE∥BC,交AC于点E,DE∥AC,交BC于点F.
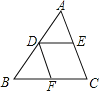
(1)求证:DE=BF;
(2)连接EF,请你猜想线段EF和AB有何关系?并对你的猜想加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=13,DE是△ABC的中位线,F是DE的中点,已知B(-1,0),C(9,0),则点F的坐标为______________.
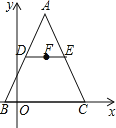
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的顶点B在反比例函数y= ![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是 .
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和5,乙口袋中装有两个相同的小球,它们的标号分别为4和9,丙口袋中装有三个相同的小球,它们的标号分别为1,6,7.从这3个口袋中各随机取出一个小球.
(1)用树形图表示所有可能出现的结果;
(2)若用取出的三个小球的标号分别表示三条线段的长,求这些线段能构成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象. 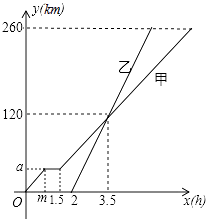
(1)求出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车行驶多长时间时,两车恰好相距50km.
查看答案和解析>>
科目:初中数学 来源: 题型:
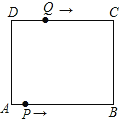
【题目】如图在长方形ABCD中,AB=12cm,BC=8cm,点P从A点出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,用x(秒)表示运动时间.
(1)求点P和点Q相遇时的x值.
(2)连接PQ,当PQ平分矩形ABCD的面积时,求运动时间x值.
(3)若点P、点Q运动到6秒时同时改变速度,点P的速度变为每秒3cm,点Q的速度为每秒1cm,求在整个运动过程中,点P、点Q在运动路线上相距路程为20cm时运动时间x值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 . 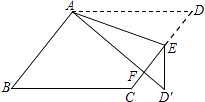
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com