
分析 (1)将x=1代入水果的售价y(元/千克)与保存时间x(天)的函数关系为y=60+2x即可求得该种水果的售价,然后乘以水果质量求得利润即可;
(2)根据利润=售价×销售量-成本列出函数关系式即可,利用配方法即可求出利润最大值.
解答 解:(1)当x=1时,y=60+2=62(元),
利润为:62×(500-10)-500×40-40=10340(元);
(2)由题意得:w=(60+2x)(500-10x)-40x-500×40
=-20x2+360x+10000
=-20(x-9)2+11620
∵0≤x≤8,x为整数,当x≤9时,w随x的增大而增大,
∴x=8时,w取最大值,w最大=11600.
答:批发商所获利润w的最大值为11600元.
点评 本题考查了二次函数的应用,解答本题的关键是仔细审题,将实际问题用函数表示出来,注意掌握配方法求二次函数最值得应用.


 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:解答题
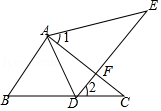 如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.
如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
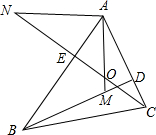 如图,在△ABC中,CE,BD为高线,M、N在BD,CE(或延长线上),且BM=AC,CN=AB.
如图,在△ABC中,CE,BD为高线,M、N在BD,CE(或延长线上),且BM=AC,CN=AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
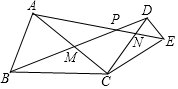 如图,△ABC和△DCE均为等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.
如图,△ABC和△DCE均为等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com