
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��20Ԫ���ۼ�Ϊÿ��30Ԫ��ÿ���¿�����180�������ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ���¾ͻ�������10������ÿ���ۼ۲��ܸ���35Ԫ����ÿ����Ʒ���ۼ�����xԪ��xΪ��������ÿ���µ���������ΪyԪ��
��1����y��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��2��ÿ����Ʒ���ۼ�Ϊ����Ԫʱ��ÿ���¿ɻ�����������������Ƕ��٣�
��3��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���µ�����ǡ����1920Ԫ��
���𰸡���1��y=��10x2+80x+1800��0��x��5����xΪ����������2��ÿ����Ʒ���ۼ�Ϊ34Ԫʱ����Ʒ���������Ϊ1960Ԫ����3���ۼ�Ϊ32Ԫʱ������Ϊ1920Ԫ��
��������
�����������1����������=ÿ����Ʒ���������180��10�����ǵ�Ǯ����������ÿ���ۼ۲��ܸ���35Ԫ���ɵ��Ա�����ȡֵ��
��2�����ù�ʽ����ϣ�1���õ��ĺ�������ʽ�ɵö��κ�������ֵ�����ʵ�����壬��������⼴�ɣ�
��3���ã�1���е�y=1920��ú��ʵ�x�Ľ⼴�ɣ�
�⣺��1��y=��30��20+x����180��10x��=��10x2+80x+1800��0��x��5����xΪ��������
��2���ɣ�1��֪��y=��10x2+80x+1800��0��x��5����xΪ��������
����10��0��
����x=![]() =4ʱ��y���=1960Ԫ��
=4ʱ��y���=1960Ԫ��
��ÿ����Ʒ���ۼ�Ϊ34Ԫ��
��ÿ����Ʒ���ۼ�Ϊ34Ԫʱ����Ʒ���������Ϊ1960Ԫ��
��3��1920=��10x2+80x+1800
x2��8x+12=0��
��x��2����x��6��=0��
���x=2��x=6��
��0��x��5��
��x=2��
��30+2=32��Ԫ��
���ۼ�Ϊ32Ԫʱ������Ϊ1920Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����8��12�ľ��������У�ÿ��С�����εı߳���Ϊ1���ı���ABCD�Ķ��㶼�ڸ���ϣ�
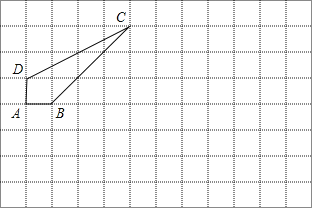
��1����BΪ����ԭ�㣬AB����ֱ��Ϊx�ᣬ����ֱ������ϵ��
��2��д���ı��θ���������ꣻ
��3�������ı��ε������
��4���������ı�������ƽ��5����λ������ƽ��2����λ�õ���ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����Ƹһ��������Ա���Լס�����λ��ѡ�˽��������Ժͱ��ԣ����ǵijɼ������
��ѡ�� | �� | �� | |
���Գɼ�(�ٷ���) | ���� | 86 | 92 |
���� | 90 | 83 | |
�����˾��Ϊ����Ϊ������Ա���Եijɼ�Ӧ�ñȱ��Եijɼ�����Ҫ�����ֱ�������6��4��Ȩ���������˵�ƽ���ɼ�����˾��¼ȡ___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������MNP�ա�NMQ��MN = 8cm, NP = 7cm, PM = 6cm, ��MQ�ij���( )
A. 8cm B. 7cm C. 6cm D. 5cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⣺��ֱ���������У�30���������Ե�ֱ�DZߵ���б�ߵ�һ�롱������������ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���ACB��90�㣬BD�ǡ�ABC�Ľ�ƽ���ߣ�P������AC������һ�� (����A��D��C�����غ�)������P��PQ��AB������ΪQ�����߶�BD��E��
(1)��ͼ�٣�����P���߶�AC��ʱ��˵����PDE����PED��
(2)������CPQ�Ľ�ƽ���߽��߶�AB�ڵ�F����PF��BD��������λ�ù�ϵ������ͼ�β�˵������.
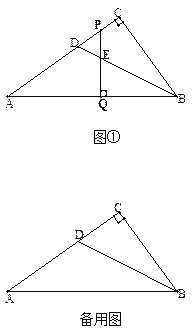
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com